Пусть дана однородная система линейных уравнений:
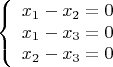
Если решать методом Гаусса - привести матрицу её коэффициентов к улучшенному ступенчатому виду, то получится просто строгоступенчатая, что означает что СЛУ определена, независимых переменных нет:
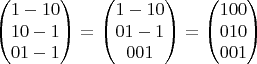
Если же не использовать метод Гаусса, выразить например

через

, то решение в общем виде будет
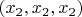
,
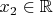
, система неопределенна.
Почему метод Гаусса и тот, который я привёл после него дают разные результаты?