Количество представлений чётных чисел суммой двух простых

[wrest]

Ende
Выделено из темы «Гипотеза о симметричных простых близнецах»

Dmitriy40
У меня вектор количеств пар до миллиона считался аж 10 минут на планшете, при том что после объяснений в соседней теме я восстановил работу gp2c и это была компилированная функция. Вы быстрее считать научились?

[Dmitriy40]

Ryzl в сообщении #1708649 писал(а):

Т.е. второй пункт тоже верен?

Нет не верен.
В какое подмножество относите пару $(199,1)$ для чётного числа $200$?

-- 08.11.2025, 21:53 --

wrest в сообщении #1708620 писал(а):

Вы быстрее считать научились?

А вот теперь научился.
Смотрите, код
q=vector(10^5); forstep(x=4,#q,2, n=0; forprime(p=3,x/2, isprime(x-p)&&n++); q[x]=n)
работает 22с.
А если в q[] накапливать количество вариантов, то код получается таким
q=vector(10^5); forprime(a=3,#q/2, forprime(b=a,#q-a, q[a+b]++))
и работает уже 14с.
А теперь финт ушами: меняем vector на vectorsmall и получаем ускорение первого варианта до 17с, а второго до 2.5с!
А поменяв порядок циклов:
q=vector(10^5); forprime(a=#q/2,#q-3, forprime(b=3,#q-a, q[a+b]++))
можно ускорить до 1.3с.
До 1е6 первый вариант считает 22м13с, второй 2м46с, а улучшенный 1м20с (все с vectorsmall).

Вероятно и это не предел.

[wrest]

Dmitriy40 в сообщении #1708651 писал(а):

Вероятно и это не предел.

Это точно не предел. ИИ тут мне полоскает мозг что если свернуть два массива то получишь что надо. Потом это сводится к возведению в квадрат полинома вида $x^2+x^3+x^5+...$ с простыми степенями, ну и всё это мгновенно. Но ходит по кругу то непопадая в индексы, то придумывая новый синтаксис для pari и я бросил затею, но там явно есть путь очень, очень быстрый.

[mihaild]

wrest в сообщении #1708660 писал(а):

Потом это сводится к возведению в квадрат полинома вида $x^2+x^3+x^5+...$ с простыми степенями, ну и всё это мгновенно

Это не мгновенно, но это за $O(N\logN)$ делается.
Алгоритм из слегка продвинутых, но широко известный. Если мы возведем в квадрат Ваш полином, то коэффициент при $x^n$ - это как раз число упорядоченных способов представить $n$ в виде суммы двух простых.
Теперь у нас есть полином $f(x)$. Давайте посчитаем $\widehat f$ - его дискретное преобразование Фурье, $\widehat f_k = f(\omega^k)$, где $\omega = \sqrt[N]{1}$. Понятно, что $\widehat{f \cdot f}_k = (\widehat f)_k^2$. Поэтому теперь наша задача сводится к вычислению дискретного преобразования Фурье. И это легко, если заметить, что для если $f = g^2$, то $f(\omega) = g(\omega^2)$, а если $f = x \cdot g^2$, то $f(\omega) = \omega \cdot g(\omega^2)$ - тем самым вычисление ДПФ для $f$ сводится к его вычислению для двух полиномов вдвое меньшей степени.
На практике это выражается в том, что scipy справляется со свёрткой 50 миллионов элементов (для ускорения процесса я взял только нечетные простые) за 19с (для калибровки - sympy на той же машине требует 2 минуты на собственно вычисление первых 100 миллионов простых).
А что дальше с этим предлагается делать?

[Dmitriy40]

Упс, мой улучшенный код (с переставленными циклами) работает неправильно.
И после исправления он такой же по скорости как и не улучшенный.

[wrest]

Dmitriy40
В общем, бинго!
Массив 10 млн считается за 9 сек в интерпретаторе (без компиляции).

1. ? g_vec(N) = { 
2.   if (N < 4, return(vector(N, k, 0))); 
3.   my(v = vector(N+1)); 
4.   forprime(p = 2, N, v[N - p + 1] = 1); 
5.   my(ff = Pol(v)^2); 
6.   vector(N, n, 
7.     if(n % 2, 0, 
8.        my(c = polcoef(ff, n)); 
9.        (c + 1) \ 2;  \\ включая самопары 
10.     ) 
11.   ); 
12. } 
13. ? gv=g_vec(10^7); 
14.   *** sqr: Warning: increasing stack size to 800000000. 
15.   *** sqr: Warning: increasing stack size to 1600000000. 
16. time = 9,714 ms. 
17. ? gv[1234568] 
18. %176 = 4843 
19. ? 

Идея проста до неприличия "и как я сразу не догадался"
Если у нас есть полином у которого единичные коэффициенты только при простых степенях, то возводя его в квадрат, получаем полином у которого в качестве коэффициентов как раз нужные нам суммы. То есть при степени 8 будет коэффициент 2 т.к. её можно получить только двумя способами: $x^3x^5+x^5x^3=2x^8$ -- делим его на два и всё. Осталось разобраться с т.н. "самопарами" когда пару составляют два одинаковых простых. Ну это тоже просто.

Спасибо Qwen-у который все-таки доделал за ChatGPT тонкости с индексированием а последнему за идею.
Вычислительнкя сложность примерно $O(\pi^2(n))$ но дикая оптимизация полиномиальной арифметики в pari делает своё дело.

-- 09.11.2025, 01:17 --

mihaild
О, пока писал свой пост, вы меня опередили с объяснением.

[mihaild]

wrest в сообщении #1708665 писал(а):

Вычислительнкя сложность примерно $O(\pi^2(n))$

Не знаю, как это реализовано в pari/gp, но вообще произведение многочленов можно посчитать за $O(NlogN)$ (тут есть некоторые хитрости с тем, что нам нужна достаточно точная вещественная арифметика, но в данном случае, когда коэффициенты сравнительно небольшие, просто float32 достаточно).

[wrest]

mihaild в сообщении #1708662 писал(а):

А что дальше с этим предлагается делать?

Ну... это было чисто вычислительное упражнение на тему "оптимизации". Свертка оказалась весьма поучительным примером. В pari/gp нет встроенной функции свертки двух рядов чисел почему-то, но есть очень быстрая (я бы даже сказал неожиданно быстрая) арифметика полиномов.

Практической целью было посмотреть какой длины бывают последовательности соседних чётных чисел такие, что вычисляемое количество пар простых уменьшается, и найти первые такие числа в уменьшающихся последовательностях.
Оказалось что первая цепочка из 4 чисел начинается с числа 620620, и дальше до 10^8 более длинных нет.
Вот она:
n=620620 pairs=5482
n=620622 pairs=5408
n=620624 pairs=2733
n=620626 pairs=2726
и дальше увеличивается:
n=620628 pairs=5420

На массиве 10^8 закончилась память (я могу отдать 8ГБайт памяти под стек pari/gp на планшете, и если отдать больше то планшету плохеет).

Ну и вообще, ТС же тут дикие заявления делал о монотонности, надо было глянуть как оно нк самом деле.

-- 09.11.2025, 01:33 --

mihaild в сообщении #1708666 писал(а):

Не знаю, как это реализовано в pari/gp, но вообще произведение многочленов можно посчитать за $O(NlogN)$ (тут есть некоторые хитрости с тем, что нам нужна достаточно точная вещественная арифметика, но в данном случае, когда коэффициенты сравнительно небольшие, просто float32 достаточно).

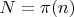
Я тоже в код не смотрел, делается ли там именно ДПФ. И там же в этом $O(NlogN)$ по сути $N=\pi(n)$ поскольку мы считаем только простые.

P.S. Я бы эти количества назвал функцией Гольдбаха. Не знаю какая от неё польза, но его имени функции нет, пусть бы была эта.

-- 09.11.2025, 02:03 --

Dmitriy40 в сообщении #1708664 писал(а):

И после исправления он такой же по скорости как и не улучшенный.

Но идея с vecsmall верная, и разрабы рекомендуют.

[Dmitriy40]

wrest в сообщении #1708667 писал(а):

И там же в этом $O(NlogN)$ по сути $N=\pi(n)$ поскольку мы считаем только простые.

По моему нет, считается весь полином, а что там много нулевых коэффициентов в ДПФ вроде бы не используется.
Вообще круто, да.

[mihaild]

Dmitriy40 в сообщении #1708671 писал(а):

По моему нет, считается весь полином, а что там много нулевых коэффициентов в ДПФ вроде бы не используется.

Более того, сами коэффициенты преобразования Фурье всё равно вряд ли часто нулевые, так что при обратном считать придётся всё.

[Dmitriy40]

wrest
Улучшил код, работает почти вдвое быстрее (потому что обрабатываются только нечётные степени):
v=vectorsmall(precprime(N-3)\2+1); forprime(p=3,#v*2-1, v[#v-p\2]=1); ff=Pol(v)^2;
q=vectorsmall(N\2,n, (polcoef(ff,n-1)+1)\2); q[2]=1;\\включая самопары, плюс коррекция N=4
Индекс n в q[n] отвечает за число 2*n.

[wrest]

Dmitriy40
Прекрасно! Для N=10^8 у меня считает 3,2 секунды в режиме интерпретации.
t_VECSMALL конечно ускоряет всё. Индекс и компоненты становятся long, и нет тяжелой машинерии арифметики произвольной точности. Думаю там ещё сколько-то можно срезать исключив polcoef, но уже не много.

[wrest]

wrest в сообщении #1708691 писал(а):

Думаю там ещё сколько-то можно срезать исключив polcoef, но уже не много.

Вот как-то так, без polcoef и без сохранения промежуточного результата возведения полинома в квадрат
v=vectorsmall(precprime(N-3)\2+1); forprime(p=3,#v*2-1, v[#v-p\2]=1);
q=apply(x->(x+1)\2,vecextract(Vecrev(Pol(v)^2),[1..N\2]));q[2]=1;
Теряется правда преимущество t_VECSMALL для вектора результата, но тем не менее это немного быстрее, у меня 2,8сек против 3,2сек для N=10^7

[Dmitriy40]

wrest
Чтобы не заморачиваться с обратной записью коэффициентов есть Polrev() вместо Pol():
v=vectorsmall(precprime(N-3)\2+1); forprime(p=3,#v*2-1, v[p\2+1]=1); ff=Polrev(v)^2;

А коэффициенты можно вернуть из t_POL вызовом Vec()/Vecsmall(), только они выдаются в обратном порядке (начиная со старших) и приходится переставлять при вычислении:
w=Vecsmall(ff); q=vectorsmall(N\2,i, (w[#w-i+1]+1)\2); q[2]=1;
И это замедляет на 5%.

-- 09.11.2025, 14:24 --

wrest
Ваш вариант требует заметно больше памяти на промежуточные результаты.

Вместо vecextract() можно написать просто
q=apply(t->(t+1)\2, Vecrev((Polrev(v)^2))[1..N\2]); q[2]=1;

[wrest]

Dmitriy40 в сообщении #1708712 писал(а):

Вместо vecextract() можно написать просто

Точно! Крутилось в голове же это.