Теория Янга Миллса

[Serg53]

Теория Янга — Миллса — Википедия
https://ru.wikipedia.org/wiki/%D0%A2%D0 ... 1%81%D0%B0

Цитата:

уравнения, описывающие эволюцию полей Янга — Миллса, являются нелинейными (в противоположность линейным уравнениям Максвелла, отвечающим абелевой теории). Можно также сказать, что для полей Янга — Миллса не выполняется принцип суперпозиции.

У меня вопрос. Как соотносятся электромагнитные поля с полями Янга — Миллса.

[realeugene]

Serg53
Какова ваша собственная попытка решения?

[yesterday]

Непонятный вопрос. Вам чистая математика нужна, про абелевы/неабелевы поля, Слабый сектор SM или...не понятно, в общем, что надо то.

[Dmitriy40]

Да непонятно человеку как из нелинейных уравнений Янга-Миллса получаются линейные Максвелла.

(Оффтоп)

Я бы предположил что это в каком-то пределе (типа для энергий ниже 100ГэВ как говорит рувики), когда все нелинейные члены уходят ниже точности экспериментов из-за высоких степеней зависимостей, либо проявляются как слабые взаимодействия, а не как электромагнитные.

[yesterday]

Только вот КЭД--это не про линейные ур-ния Максвелла. Там нелинейная динамика. (В этом и отличие КЭД от линейных ур М.). Она про абелевы поля просто. А ТС хочет неабелевы, судя по всему

[Xugin]

(Оффтоп)

На днях, нестало автора этой теории, Чженьнина Янга...

[pppppppo_98]

Serg53 в сообщении #1707244 писал(а):

меня вопрос. Как соотносятся электромагнитные поля с полями Янга — Миллса.

электромагнитное поле - простейшее их калибровочных полей (Янга-Миллса в вашей терминологии), с абелевой группой симметрии U(1) - тоже простейшей из всех компактных групп Ли

-- Пн окт 27, 2025 15:57:45 --

Dmitriy40 в сообщении #1707253 писал(а):

Да непонятно человеку как из нелинейных уравнений Янга-Миллса получаются линейные Максвелла.

дык никак... они изначально линейные, по крайне мере в простейшей теории

-- Пн окт 27, 2025 16:04:51 --

Xugin в сообщении #1707284 писал(а):

На днях, нестало автора этой теории, Чженьнина Янга...

(Оффтоп)

Земля пухом

Их миллион всяких фолиантов по калибровочным полям, полистайте. Мне понравился геометрический подход у Баеза. http://home.ustc.edu.cn/~zcj12138/refer ... ravity.pdf

[Serg53]

yesterday в сообщении #1707254 писал(а):

КЭД--это не про линейные ур-ния Максвелла. Там нелинейная динамика. (В этом и отличие КЭД от линейных ур М.)

Извините за дилетантский вопрос. Являются ли электромагнитные поля частным случаем полей Янга — Миллса?

[yesterday]

Цитата:

Являются ли электромагнитные поля частным случаем полей Янга — Миллса?

Если вопрос только в терминах, то не знаю. Когда я в аспе писал кандмин по истории науки, то полями ЯМ называли только неабелевы теории, исторически.
Хотя, вот оратор выше говорит, что абелево поле с симметрией $U(1)$ тоже является частным случаем полей ЯМ.

В принципе, да какая разница, как называть, при условии, что все понимают одно и тоже. Если уж терминологический спор, то--"теории типа ЯМ--это про неабелевы поля", как теория слабых взаимодействий и КХД. Так исторически сложилось

Но мне почему-то кажется, что вопрос в другом. Как из неабелевой теории электрослабых взаимодействий получается КЭД. Или я не прав?

[Alex-Yu]

Serg53 в сообщении #1707832 писал(а):

Являются ли электромагнитные поля частным случаем полей Янга — Миллса?

Нет. Это абелево калибровочное поле. А поля Янга-Милса -- это неабелевы калибровочные поля. Точнее даже не так: поле Янга-Милса это поле с калибровочной группой $SU(2)$. Именно такое поле рассматривали Янг и Милс в очень далеких годах (не помню точно, то ли в 50-х, то ли самое начало 60-х 20 века). Но как-то прижилось называть полями Янга-Милса калибровочные поля с любой неабелевой калибровочной группой. Хотя для случая отличного от $SU(2)$ правильнее было бы сказать поля типа полей Янга-Милса (похоже, но не в точности то же самое).

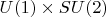
Хотя, конечно, есть электрослабая теория, в которой есть электромагнитный сектор. Хотя изначально группа электрослабой теории неабелева. Правда, в той группе есть абелева подгруппа $U(1)$, но, во-первых, это не электромагнитная группа, во-вторых, в целом группа $U(1) \times SU(2)$ все же неабелева. А в третьих, электромагнитный сектор электрослабой теории -- это все же не то же самое, что "чистая" электродинамика. И да, еще. Даже в "чистой" электродинамике взаимодействие с фермионами приводит к тому, что уравнения уже не являются линейными. Электродинамика была бы линейной, если бы ЭМ поле ни с чем бы не взаимодействовало. Уже даже в классике.