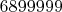Найдите 2025-е по счёту замечательное число

[gipokrat]

Назовём натуральное число замечательным, если оно самое маленькое среди натуральных чисел с таким же, как у него, произведением цифр.
Перед вами первые 20 замечательных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 25, 26, 27, 28, 29, 35, 37, 38, 39, 45. Этой последовательности, как и следовало ожидать, нет в OEIS.
Найдите 2025-е по счёту замечательное число!

[mihaild]

Навскидку замечательных чисел из $N$ разрядов примерно $C_{N-1}^3$ (цифр кроме 5789 максимум одна-две), так что понадобится что-то в районе 20 цифр. Наверное можно аккуратно посчитать руками, но не очень хочется.

[gipokrat]

mihaild
Нет, намного меньше 20.

[Booker48]

Разве это не значит, что нужно найти минимальное число, у которого в 10-ной записи произведение цифр равно 2024?

upd

Понял, вопрос снят.

[wrest]

Booker48 в сообщении #1706733 писал(а):

которого в 10-ной записи произведение цифр равно 2024

Таких чисел не бывает

[mihaild]

Понятно что цифры отсортированы. Вроде бы может быть произвольное количество 5789, плюс один из вариантов: 2,4,6,26.
Итого $N$-значных чисел $C_{N + 3}^3 + 3 \cdot C_{N + 2}^3 + C_{N + 1}^3$ (я в прошлом сообщении неправильно число композиций записал).

[wrest]

mihaild в сообщении #1706729 писал(а):

Найдите 2025-е по счёту замечательное число!

Ответ:

(Оффтоп)

3555555555

-- 22.10.2025, 14:40 --

Функция pari/gp mn(p) возвращает минимальное число, произведение цифр десятичной записи которого равно p, или возвращает ноль, если такого числа не существует.

mn(p) =
{
  if (p == 0, return(10));
  if (p == 1, return(1));
  my(v = []);
  forstep(d = 9, 2, -1,
    while (p % d == 0, v = concat(v, d); p /= d;)
  );
  if (p != 1, return(0));
  return(fromdigits(Vecrev(v)));
};

[Dendr]

Возьмем произвольное число, не содержащее в десятичной записи нолей и "минимизируем" его - то есть так заменим цифры, чтобы сохранить произведение. Понятно, что первый шаг - расставить цифры по неубыванию. Единицы в начале можно выкинуть.
Далее поступаем так: ищем пары цифр и менять их (оставляя на своих местах) на другие, так, чтобы "двузначное" число (хотя и разделенное рядом цифр) уменьшилось.
$22\to14, 23\to16, 24\to18, 33\to19, 34\to26$
$ 36\to29, 44\to28, 46\to38, 66\to49$
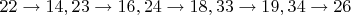
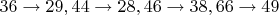
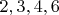
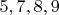
После этого "пузырьком" опять упорядочиваем. Видно, что цифры $2, 3, 4, 6$ теперь встречаются только по разу, зато $5, 7, 8, 9$ только копятся. Игнорируем их пока.
Есть возможности - $-, 2, 3, 4, 6, 23, 24, 26, 34, 36, 46$. Они сводятся еще одним шагом и отбрасыванием, если надо, единиц и "копящихся" цифр, к набору $-, 2, 3, 4, 6, 26$

Таким образом, все замечательные числа, большие $10$, можно разбить на виды:

$$(5)(7)(8)(9)$$

$$2(5)(7)(8)(9)$$

$$3(5)(7)(8)(9)$$

$$4(5)(7)(8)(9)$$

$$(5)6(7)(8)(9)$$

$$2(5)6(7)(8)(9)$$

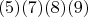
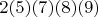
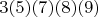
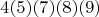
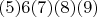
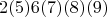
Где цифры в скобках - это несколько повторяющихся цифр (возможно, ноль).
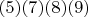
Пусть $F(n)$ - количество чисел вида $(5)(7)(8)(9)$, состоящие из $n$ цифр. Тогда $G(n)$ - количество $n$-значных замечательных чисел:

$$G(n)=F(n)+4F(n-1)+F(n-2)$$

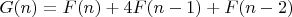
Понятно, что $F(n)=\frac{(n+1)(n+2)(n+3)}{6}$
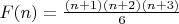
Значит, $G(n)=\frac{(n+1)(n+2)(n+3)}{6}+\frac{4n(n+1)(n+2)}{6}+\frac{(n-1)n(n+1)}{6}=(n+1)^3$

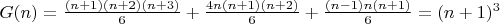
Ну и прекрасно...
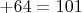
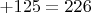
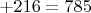
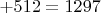
Десятое число - $10$, добавляем двузначные - $+27 = 37$, трехзначные - $+64 = 101$, четыре- $+125 = 226$, пяти- $+216 = 785$, шести- $+512 = 1297$, семи- $+729 = 2026$.

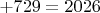
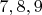
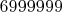
Еще лучше! Значит, это предпоследнее семизначное. Обращаясь к табличке выше, делаем вывод, что оно должно начинаться на шестерку (пятая строка, с пустым множеством пятерок), после которой еще 6 цифр (из набора $7, 8, 9$). Последнее, очевидно, $6999999$ - последнее, значит, перед ним идет $6899999$

[mihaild]

Подсчет хороший (интересно, почему так хорошо сворачивается?..), пара мелких ошибок.

Dendr в сообщении #1706757 писал(а):

четыре- $+125 = 226$, пяти- $+216 = 785$, шести- $+512 = 1297$, семи- $+729 = 2026$.

Вот тут сбились на единицу в числе разрядов. Пятиразрядные $+216 = 442$, шестиразрядные $+343 = 785$. И в итоге восьмизначное число.

Dendr в сообщении #1706757 писал(а):

Значит, это предпоследнее семизначное. Обращаясь к табличке выше, делаем вывод, что оно должно начинаться на шестерку

Последнее число с данным количеством разрядов состоит из одних девяток, а перед ним - из одной восьмерки и девяток.

[Booker48]

gipokrat в сообщении #1706721 писал(а):

Этой последовательности, как и следовало ожидать, нет в OEIS.

Зато есть последовательность A002473, 7-smooth numbers: positive numbers whose prime divisors are all <= 7.
Находим в последовательности $2025$-е число, это $7503125 = 5^5 7^4$
Соответственно, $2025$-е замечательное будет $555557777$.

[mihaild]

Booker48 в сообщении #1706771 писал(а):

Соответственно, $2025$-е замечательное будет $555557777$

Это так не работает. У меньшего замечательного числа может быть большее произведение цифр, чем у большего.

[Booker48]

mihaild в сообщении #1706772 писал(а):

Booker48 в сообщении #1706771 писал(а):

Соответственно, $2025$-е замечательное будет $555557777$

Это так не работает. У меньшего замечательного числа может быть большее произведение цифр, чем у большего.

Понял, спасибо.

[gris]

у Энцикопедии есть загадочное свойство начинать счётчик с нуля и тогда последовательность отыскивается, и ея 2025-тый элемент можно увидеть. Но теоретические выкладки, конечно, красившее.
А я нашёл это дело по-простому, перебирая все числа до 10 млрд.
{n=666;
s=Set(1);p=vector(2030);p[1]=1;ls=1;
for(i=1,10^10,
m=vecprod(digits(i));
s=setunion(s,Set(m));
if(#s>ls,
ls++;p[ls]=i;
if(ls==n,print(ls," ",i," ",m);break)
)
)}
666 555777 42875
time = 12,496 ms.
Для 2025 нужна доступная оптимизация .

[wrest]

mihaild в сообщении #1706758 писал(а):

И в итоге восьмизначное число.

Ага. Предпоследнее.

-- 22.10.2025, 20:39 --

wrest в сообщении #1706744 писал(а):

Ответ:

Тот ответ неверный. Верный - предпоследнее 8-значное

-- 22.10.2025, 20:41 --

gris в сообщении #1706779 писал(а):

Для 2025 нужна доступная оптимизация .

Вы можете перебирать числа и считать произведения цифр, а можете перебирать произведения и по ним вычислять минимальные числа.

-- 22.10.2025, 20:43 --

Как видите,

gris в сообщении #1706779 писал(а):

666 555777 42875

произведение в случае 666 на порядок меньше самого числа

-- 22.10.2025, 21:00 --

gris
Вот вам функция которая определяет, является ли произведение допустимым.

is_prod(n)=
{
if(n<10,return(1)); // от нуля до 9 все есть
forstep(d=9,2,-1,while(n%d==0;n/=d;)); //пока делится, делим на 9,8,7...2
if(n==1,return(1),return(0)) //если разделилось, значит произведение годное, иначе негодное
}

[wrest]

Учусь считать эти числа.
Если кто уже умеет, то 1 000 000-е замечательное число у меня получилось равным
25555577777777777777777777778888888888888899 - проверьте пож-ста