Найдите 2025-е по счёту замечательное число

[wrest]

Асимптотическая сложность $O(\sqrt[4]{n})$ что конечно похуже логарифма, но тоже весьма достойно, я считаю. При том что по памяти сложность $O(1)$

Наверное попробую улучшить и до логарифма, тогда это будет идеальный алгоритм (т.к. результат как раз логарифмического размера).
Но пока не получается.

[wrest]

Дописал, при помощи ИИ, алгоритм который считает за O(log(n)).

(Оффтоп)

1. comb_fast(n)={  
2. /* функция возвращает вектор кратностей цифр n-го замечательного числа */  
3. /* входной контроль */  
4. if(n<1,error("n must be positive, got n=",n));  
5. /* нерегулярные случаи */  
6. if(n<10,return([[n,1]]));  
7. if(n==10,return([[1,1],[0,1]])); /* тут по неубыванию не выходит */  
8.   
9. /* начало основного вычисления */  
10. my(len=floor((sqrt(8*sqrt(n-2)+1)-1)/2)); /* вычисляем длину числа -- количество цифр в нём */  
11. my(npos=n-len^2*(len+1)^2/4-1); /* вычисляем относительную позицию числа где единица -- начало ряда чисел нашей длины */  
12.   
13.      /* Определяем фиксированные цифры */  
14.     my(fixed_digits = vector(7));  
15.     fixed_digits[1] = [[2, 1]];      /* тип 1 */  
16.     fixed_digits[2] = [[2, 1], [6, 1]];  /* тип 2 */  
17.     fixed_digits[3] = [[3, 1]];      /* тип 3 */  
18.     fixed_digits[4] = [[4, 1]];      /* тип 4 */  
19.     fixed_digits[5] = [];            /* тип 5 */  
20.     fixed_digits[6] = [[6, 1]];      /* тип 6 */  
21.       
22.     /* Вычисляем размеры диапазонов для каждого из 6 типов*/  
23.     my(type_len=vector(6,i,len-#fixed_digits[i])); /* длина сочетания равна длине числа минус количество фиксированных цифр */  
24.     my(type_range=vector(6,i,(type_len[i]+1)*(type_len[i]+2)*(type_len[i]+3)/6)); /* тетраэдральные числа */  
25.     my(type_finish=vector(6,i,sum(j=1,i,type_range[j]))); /* концы диапазонов шаблонов */  
26.   
27.   /* Определяем тип числа */  
28.     my(type_num, type_pos);  
29.     if(npos <= type_finish[2],  
30.         type_num = 2; type_pos = npos;  
31.     , npos <= type_finish[3],  
32.         type_num = 3; type_pos = npos - type_finish[2];  
33.     , npos <= type_finish[4],  
34.         type_num = 4; type_pos = npos - type_finish[3];  
35.     , npos <= type_finish[6],  
36.         type_num = 6; type_pos = npos - type_finish[4];  
37.     ,  
38.         error("npos too big: ", npos)  
39.     );  
40.   
41.  /* Обрабатываем составные типы 12 и 56, которые идут вперемешку */  
42.    
43.     if(type_num == 2 || type_num == 6,   
44.         my(m = floor((3*type_pos)^(1/3))); /* примерно куб, иначе пришлось бы по формуле Кардано */  
45.         if(m*(m+1)*(m+2)/3 >= type_pos, m--); /* если не попали, корректируемся */  
46.           
47.         my(Sm = m*(m+1)*(m+2)/6);  
48.         my(offset = type_pos - 2*Sm);  
49.         my(L = (m+1)*(m+2)/2);  
50.           
51.         my(subtype = if(offset <= L, 1, 0));  
52.         type_pos = Sm + if(subtype == 1, offset, offset - L);  
53.           
54.         /* Преобразуем в окончательный тип 1 2 или 5 6*/  
55.         type_num=type_num-subtype;  
56. );  
57.   
58.     /* начинаем вычислять кратности цифр 5789 */  
59.    my(elts=[5,7,8,9]); /* вектор элементов для генерации их сочетания */      
60.    my(v_mult=vector(#elts,i,vector(2))); /* заготавливаем вектор кратностей цифр 5789 */  
61.       
62.     /*   
63.    Вычисляем вектор кратностей для сочетания с повторениями  
64.    номер type_pos, из #elts элементов по type_len[type_num], в лексикографическом порядке   
65.    по неубывающим  последовательностям (т.е. сначала все минимальные элементы).  
66. */  
67.   my(n_elts=#elts);  
68.   my(m = n_elts + type_len[type_num] - 1, t = n_elts - 1, total = binomial(m, t));  
69.  
70.   
71.   /* приводим type_pos к 0-based */  
72.   type_pos = type_pos - 1;  
73.   
74.   /* инвертируем позицию, чтобы порядок стал лексикографическим по неубыванию --- */  
75.   type_pos = total - 1 - type_pos;  
76.  
77.   /* выбираем позиции перегородок (1..m) */  
78.   my(seps = vector(t), prev = 0, bincount=0); 
79.   for (j = 1, t, 
80.     my(low = prev + 1, high = m - (t - j), Rtj = t - j); 
81.  
82.     /* бинарный поиск: ищем минимальный s в [low..high], такой что 
83.        prefix(low..s) > r, где 
84.        prefix(low..mid) = C(m-low+1, Rtj+1) - C(m-mid, Rtj+1) */ 
85.     my(A = m - low + 1, pref_high, pref_mid); 
86.     while (low < high, 
87.       my(mid = (low + high) \ 2); 
88.       pref_mid = binomial(A, Rtj+1) - binomial(m - mid, Rtj+1); bincount+=2; 
89.       if (pref_mid > type_pos, 
90.         high = mid;       /* возможно ответ слева включительно */ 
91.       , 
92.         low = mid + 1;    /* префикс до mid <= r, идём правее */ 
93.       ); 
94.     ); 
95.     seps[j] = low; 
96.  
97.     /* вычитаем из r все варианты, которые мы прошли (skip = prefix(low-1)) */ 
98.     if (low > prev + 1, 
99.       my(skip = ( binomial(m - (prev + 1) + 1, Rtj + 1) - binomial(m - (low - 1), Rtj + 1) ));bincount+=2; 
100.       type_pos = type_pos-skip; 
101.     ); /* иначе skip = 0 */ 
102.  
103.     prev = low; 
104.   ); 
105.   
106.   /* переводим позиции перегородок в кратности (число звёзд между ними) */  
107.     
108.   for(i=1,n_elts,v_mult[i][1]=elts[i]);  
109.   v_mult[1][2] = seps[1] - 1;  
110.   for (j = 2, t, v_mult[j][2] = seps[j] - seps[j-1] - 1);  
111.   v_mult[n_elts][2] = m - seps[t];  
112.   /* добавляем фиксированные цифры и сортируем результат по неубыванию */  
113.    v_mult = vecsort(concat(v_mult, fixed_digits[type_num])); /* в принципе, готовои ещё чуть: */  
114.    
115.      /* удаляем нулевые кратности */  
116.      my(res=[]);  
117.      for(i=1,#v_mult,if(v_mult[i][2]>0,res=concat(res,[v_mult[i]])));  
118.   
119.      return(res);  
120. }  

Запуск:

? comb_fast(20^25)
time = 4 ms.
%191 = [[3, 1], [5, 1420700], [7, 16335714], [8, 136434330], [9, 37213898]]
? comb_fast(10^1025);
time = 17 ms.
?

В общем решил повысить ставки до 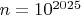$n=10^{2025}$
17 миллисекунд вычисляется замечательное число номер 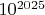$10^{2025}$, если подавить печать (напечатанное не помещается на поля этого форума).

В общем - всё. Алгоритм асимптотически идеальный. Улучшить нельзя теоретически.