То, что математики опять же опустили фигурные скобки вокруг пустоты(нуля) и заменили их на перечеркивание нуля
Извините, но для меня это звучит как бред.

и

— это просто два (из многих других) обозначения пустого множества, применяемых в разной литературе разными авторами. Никакого "потаённого" смысла в этих обозначениях нет. Иметь специальное обозначение для пустого множества необходимо, так как, во-первых, это константа, необходимая для формулировки аксиом теории множеств, а во-вторых, оно очень часто встречается в любых рассуждениях, касающихся множеств. Каким именно значком обозначать пустое множество, не имеет никакого значения. Если я буду писать статью и напишу в ней, что "будем обозначать пустое множество вот этой закорючкой", то никто возражать не будет. Кроме издательства, у которого в типографии такой "закорючки" может не найтись.
Обозначения обусловливаются конвенцией. Тут я с Вами согласен. Но единообразность и унификация обозначений - это благо. Достаточно уже того, что 0 - это особый элемент среди чисел и имеет свой значек, чтобы с его помощью обозначить особое пустое множество.
Вам не кажется, что, прежде чем браться за реформирование теории множеств, следует в ней очень хорошо разобраться? И, в частности, понять, что теория множеств может смоделировать практически любую математическую конструкцию.
Я понимаю, что теория множеств может смоделировать почти любую конструкцию. Но опять же, цель- унификация и единообразие всех конструкций, уменьшение до минимума понятий и определений.
Понимаю, что прежде чем браться за что-то и реформировать что-то, надо очень хорошо в этом разобраться, но у меня мало времени, чтобы разбираться и если этим заниматься основательно, то на реформы его не останется)))
В моем понимании
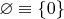
В стандартном понимании — нет, и никто вашу "идею" не примет. Потому что она категорически нарушает смысл теории множеств. Множество включает только то, что ему принадлежит, и не нужно пихать в него то, чего в нём нет. Если
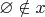
, то
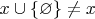
(конечно,
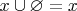
для любого множества

).
Не совсем понял, что Вы имеете ввиду. Не по ошибке ли Вы перечеркнули значек принадлежности?
Мне кажется у Вас тут парадокс. Если пустое множество не входит в качестве элемента во множество, то объединение множества и пустого множества не равно множеству, а это объединение всегда равно множеству,
следовательно пустое множество всегда входит в множество в качестве элемента, жирным добавлено мной. Или я неправильно понимаю? По сути, Вы доказали мою правоту?

- множества не удовлетворяющие аксиоме регулярности. стрелка - биекция. Любой элемент множества
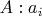
равен множеству

или биективно на него отображается, а это значит, что он сам является множеством, состоящим из элементов, которые являются равными ему и т.д., и т.д.
Извините, но это тоже бред. Каждый элемент множества равен ему самому, следовательно, все элементы множества равны, а так как Вы в каждое множество впихнули ещё и пустое множество, то, следовательно, все они равны пустому множеству, и все множества — пустые. Шикарно. Вселенная, в которой ничего нет.
Я показал, что это не так в первом посте, потому, что из Вселенной в которой ничего кроме скобок нет, извлекаем кусочки: натуральные, вещественные, функции и т.д. и они от этого извлечения появляются и мы с ними работаем. И не только мы их можем извлекать, поэтому Вселенная состоит из этих обрывков, которые подчиняются закономерностям и законам.