Непонятно:
1. Почему два интеграла равны?
2. Почему
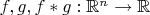
, хотя тут есть две переменные

и

? Они входят в

переменных?
3. Смысл свёртки
4. Зачем она нужна была аж Эйлеру в 18 веке и остальным позже?
1. Потому, что интегрируем от минус до плюс бесконечности.
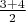
. Одномерная свёртка: Вы ударник в рок-группе. Ваши удары по барабану можно записать функцией

. Каждый удар порождает звук

, где g - отклик на единичный импульс. Ваши слушатели слышат свёртку этих двух функций.
Двумерная свёртка: Вы американский шпион (спутник-шпион), подсматривающий за РВСН России через телескоп. Свет на входе телескопа

, но объектив телескопа имеет искажения, выражающиеся функцией

. На ПЗС-матрицу поступает свёртка этих функций (зная аппаратную функцию объектива

можно попытаться восстановить истинное изображение)
Трёхмерная свёртка: в Вашем мозгу в каждой его точке в момент t приходят нервные импульсы

, на которые нейрон реагирует ответом

, который мы пишем в виде ЭЭГ (на самом деле тут надо и развёртывание во времени учитывать)
То есть существует великое множество задач из физики и родственных наук, где имеет место процесс свёртки и нужно его описывать и изучать свойства.