Смысл операции свёртки

[skobar]

Red_Herring в сообщении #1705780 писал(а):

Свертка с данной функцией $g$ это линейный оператор $A$ инвариантный относительно (всех) сдвигов $T_h^{-1}AT_h = A $

Вот это понятно. Но amon сказал совсем другое. Все вопросы остаются в силе.

[Mihaylo]

skobar в сообщении #1705777 писал(а):

А то вдруг "свертка в машинном обучении" и свертка в функане (определение которой вы привели) - это две разные свертки?

Это две разные свёртки, не обращайте внимание.

[dsge]

Mihaylo
Если вас интересует свёрточная нейронная сеть, там речь идет о дискретных свертках. В английской вики есть соответсвующий раздел - Discrete convolution.
https://en.wikipedia.org/wiki/Convolution

-- 13.10.2025, 21:47 --

Mihaylo в сообщении #1705784 писал(а):

о две разные свёртки, не обращайте внимание.

Они не разные, просто одна дискретная версия другой, интеграл заменяется суммой.

В теории вероятностей есть дискретные и непрерывные случайные величины. Чтобы найти плотность непрерывной или распределения дискретной случайной величины для суммы двух случайных величин непрерывных или дискретных, надо взять свертку непрерывную или дискретную, соответственно.

[skobar]

dsge в сообщении #1705785 писал(а):

Если вас интерисует свёрточная нейронная сеть, там речь идет о дискретных свертках. В английской вики есть соответсвующий раздел - Discrete convolution. https://en.wikipedia.org/wiki/Convolution

В ссылке точно такое же определение свертки

[dsge]

skobar в сообщении #1705786 писал(а):

В ссылке точно такое же определение свертки

И я о том же.

[amon]

skobar в сообщении #1705777 писал(а):

Дайте определение "однородного координатного пространства" и поясните, что такое "общий вид линейного оператора" на нем и как он вдруг становится сверткой, которая по определению двум функциям из какого-то пространства сопоставляет третью функцию.

Мы чего-то объяснить пытаемся, или меряемся кто лучше функциональный анализ знает? Я не сомневаюсь, что Вы его лучше знаете. Есть у нас уравнение Пуассона в 3-х мерном пространстве.

$$\Delta\varphi=4\pi\rho.$$

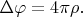
Его функция Грина -
$G(\mathbf{r,r'})=\frac{1}{|\mathbf{r}-\mathbf{r}'|}.$
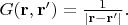
Обратный оператор, восстанавливающий $\varphi$ по заданному $\rho$ -

$$\varphi(\mathbf{r})=\int d^3y\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}.$$

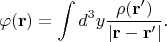
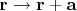
Координатное пространство в данном случае $\mathbb{R}^3.$ Однородность означает, что сдвиг начала координат (замена $\mathbf{r}\to\mathbf{r}+\mathbf{a}$ в операторе Лапласа и аргументах функций) не поменяет уравнения, и все, что надо для того, чтобы получить решение для сдвинутого распределения плотности - сдвинуть аргумент $\varphi.$ На физическом птичьем языке это называется однородностью пространства. Причем "пространством" называется не пространство функций $L^2$ а обычное окружающее нас, которое задает координаты точки (аргумент функции). 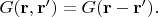Следствием этой однородности является то, что функция Грина зависит только от разности аргументов, а не от каждого по отдельности $G(\mathbf{r,r'})=G(\mathbf{r}-\mathbf{r}').$ Тогда ответ имеет вид свертки, причем одна из функций фиксирована "навсегда". Именно такой вариант использования сверток в народном хозяйстве я и имел в виду, когда отвечал на вопрос ТС "зачем нужна свертка". Широкого применения ее в физике и прочем народном хозяйстве для случая, когда обе функции не фиксированы я сразу и не вспомню.
В гильбертовом пространстве $L^2$ с интегральным скалярным произведением любой линейный оператор, насколько я помню, представим как
$\hat A \Psi=\int A(x,x')\Psi(x')dx'.$
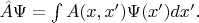
Если $\hat A$ не меняется при сдвиге $x,$ то ядро интегрального оператора зависит только от разности аргументов, и интеграл будет сверткой.

[dsge]

Mihaylo в сообщении #1705770 писал(а):

Это свёртка в машинном обучении так преподаётся.

Для сверточных нейронных сетей, свертка, по сути, усредняет близлежайшие пиксели.

[skobar]

amon в сообщении #1705789 писал(а):

Именно такой вариант использования сверток в народном хозяйстве я и имел в виду, когда отвечал на вопрос ТС "зачем нужна свертка"

Как раз это я более-менее понял, мои вопросы были другие. Ладно, бесполезно добиваться от физика математической строгости изложения, так что оставим это.

[skobar]

Mihaylo в сообщении #1705784 писал(а):

Это две разные свёртки, не обращайте внимание.

Похоже, что свертка все-таки одна и та же, но у вас, как уже отметил dsge, используется в основном дискретный случай.
Есть очень хорошее видео, где идея свертки объясняется на пальцах - то, что вам нужно, но оно на английском. Раньше канал переводился на русский, но несколько лет назад перестали это делать:
https://youtu.be/KuXjwB4LzSA?si=tzYjBffLdugFhCwK
На канале вообще много замечательных интересных обучающих роликов.

[Евгений Машеров]

amon в сообщении #1705789 писал(а):

Широкого применения ее в физике и прочем народном хозяйстве для случая, когда обе функции не фиксированы я сразу и не вспомню.

Blind deconvolution.
Неизвестный сигнал передан по каналу с неизвестной функцией отклика на единичный импульс. Восстановить исходный по принятому сигналу (который свёртка исходного сигнала с функцией отклика)

[Mihaylo]

dsge в сообщении #1705790 писал(а):

Для сверточных нейронных сетей, свертка, по сути, усредняет близлежайшие пиксели.

Это неверная трактовка. В нейронных сетях одну из "функций" свёртки - ядро - можно рассматривать как усилитель/подавитель. Ядро имеет небольшую размерность (9-25 значений), располагают квадратиком, и этот квадратик пробегает по функции гораздо большей размерности. Если где-то на участке происходит хорошее совпадение ядра со входной функцией, то в результирующей функции будет высокое значение - соответствующий нейрон с следующем слое возбудится.

Да, это другое - дискретная свёртка.

[Евгений Машеров]

dsge в сообщении #1705790 писал(а):

Для сверточных нейронных сетей, свертка, по сути, усредняет близлежайшие пиксели.

Совершенно не обязательно. Можно и операцию дифференцирования реализовать в виде свёртки с соответствующими коэффициентами, не только "усреднять". А вообще там скорее "сопоставление с образцом".

[dsge]

Евгений Машеров в сообщении #1705816 писал(а):

dsge в сообщении #1705790 писал(а):

Для сверточных нейронных сетей, свертка, по сути, усредняет близлежайшие пиксели.

Совершенно не обязательно. Можно и операцию дифференцирования реализовать в виде свёртки с соответствующими коэффициентами, не только "усреднять".

Да, в некоторых случаях:
https://en.wikipedia.org/wiki/Pooling_layer
(Average pooling)