Теперь пройдём последний этап – доказательство Леммы III.
Дам некоторую раскладку ключевых ходов при выводе этой леммы.
Из-за машинных шаблонов обозначения в моём пояснении существенно отличны от тех, что в основном тексте, но по смыслу, надеюсь, читатель восстановит сооответствие обозначений. В частности, буква

в обозначении

здесь употребляется вместо заглавной буквы [Эс] шрифта Brush Script.
Для произвольного

-конечного

-множества



, собранного из

-линий
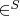

(см. предыдущие пояснения) существует, определено некоторое

-множество

,

-элементы которого суть те

-ординалы, которые суть

-номера

-сопоствлений,

-сопоставляющих

-множество

некоему другому

-конечному

-множеству

,

-элемементы которого суть

-линии
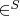

. Считаем при этом, что
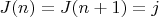
. Образуем

-множество

, составленное из таких

-конечных

-множеств

(

-принадлежащих множеству

), для которых, для каждого натурального числа

значение

есть конечное подмножество множества

. Тем самым,

есть метазамыкание для множества

. Это означает, что для всякого

-конечного

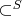

существует такая

-счётная цепочка множеств



,



, что для каждого



верно
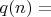


(с точностью до

-равного

-множеству

), и также
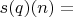





(также с точностью до

-равного). Пусть

– произвольное

-конечное

-множество,

-элементы которого

-конечные

-подмножества

-множества

(

использована вместо жирной курсивной буквы
f из основного текста доказательства Лемммы III).

-Объединение всех

-элементов,

-принадлежащих

-множеству

, обозначим

. Тогда, с точностью до

-равного

-множеству

, всегда можно указать счётную цепочку

-конечных

-множеств

, взятых из множества

, и таких, что для каждого натурального числа

множество

в точности есть объединение множеств


,


, …,
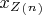

, т.е. Множества


,


, …,
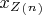

в точности есть все элементы множества

. При том, пусть
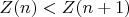
. Если мы докажем лемму для такого рода

-множества

, то тем более она верна и для всех других указанных

. Тогда, по лемме II, для некоторого

-ординала

, который принадлежит классу

, получаем, что


-сопоставляется

-ым

-сопоставлением (точнее,

-сопоставляется

-сужением такого

-сопоставления, но здесь в пояснении мы упрощаем фразы) некоему

-множеству

, собранному из

-линий
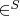

, как из

-элементов. При том,

сопоставляется


-ым сопоставлением множеству



для всех достатчно больших значений аргумента



. Тогда, все множества





,





, …,


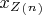


пересекаются по этому


для всех достаточно больших



. Произвольное

-множество

,

-принадлежащее

, тогда (с точностью до

-равного) можно считать последовательностью со значениями
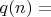
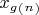

, где натуральное число

не превышает числа

. Функция

конечно же однозначно определяет

-множество

(с точностью до

-равного). Следовательно, для всех достаточно больших



, множество
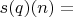


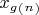


содержит ординал


. Ч.т.д. (с точностью до того, что приведено всё же только пояснение ключа доказательства).
Замечу немаловажное. Теория

полностью является частью теории
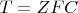
. Т.е. каждая формула


есть формула теории

, все предметы теории

суть предметы теории

. Кроме того, по теореме 11, если средствами теории

доказано некоторое

-утверждение, то

-утверждение


, знаковосоответствующее доказанному в

, также доказуемо в теории

. Тем самым, доказанная в итоге теорема, аналогичная Аксиоме I, есть теорема ZFC.