на диаграмме 1 изображена система зеркал, движущаяся в плоскости
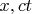
, куда и как поворачиваются эти зеркала?
На диаграмме 1 зеркала никуда не поворачиваются. И движутся те зеркала не в плоскости
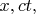
а в 3-мерном пространстве с координатами

Там зеркальные поверхности всё время параллельны плоскости
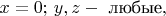
то есть зеркала перпендикулярны оси

Вектор скорости

каждой точки, принадлежащей любой из двух движущихся зеркальных поверхностей, параллелен оси

в том примере его проекции на координатные оси есть:
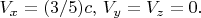
И применимо ли здесь вообще пользоваться такими терминами как отражение или отскок, если законы отражения не выполняются?
В тех примерах, которые выше были проиллюстрированы ПВ-диаграммами, всё, что движется, оно движется параллельно оси

Вдоль неё или в противоположном направлении. Оси

системы покоя зеркал параллельны соответственно осям

так что и в системе покоя зеркал отскоки и отражения в тех примерах происходят в направлении, перпендикулярном зеркалам. Все законы выполняются.
А вообще, в любом случае можно говорить об отражении чего-нибудь от чего-нибудь, если оно не поглощается и не проходит насквозь. Рассеяние света матовой поверхностью это тоже своего рода отражение. Можно говорить и о лишь частичном отражении, частичном поглощении и частичном прохождении. С мячиком аналогично: если он не прилипает к стенке и не прошибает её насквозь, значит отскакивает (можно сказать, "отражается" от стенки). Важно правильно количественно описывать явления, а названия это уже второстепенное дело, терминология - вопрос привычки и традиций.
На ПВ-диаграммах ничего не движется. Это графики уже свершившихся движений или тех, которые в рассматриваемой теоретической задаче заведомо произойдут (вследствие постановки задачи). В примерах с движением вдоль одной только оси

бывает достаточно рассматривать такие графики с осью абсцисс

и осью ординат

в заданной ИСО. Или с осью абсцисс

и осью ординат

в другой ИСО. При большой (в смысле не пренебрежимо малой по сравнению c

скорости движения одной ИСО относительно другой, оси

и

выглядят некоторым образом повёрнутыми (наклонёнными) на ПВ-диаграмме

а оси

и

выглядят повёрнутыми (наклонёнными) на ПВ-диаграмме

Так наглядно проявляется "поворот в пространстве-времени", о котором нередко говорят в связи с преобразованиями Лоренца. Более строго термин "поворот" в этом контексте поясняется формулами. Например, при повороте радиус-вектора с компонентами

на плоскости с обычной евклидовой геометрией остаётся неизменным квадрат длины радиус вектора:
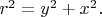
Аналогично этому, на плоскости
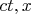
с геометрией Минковского при "повороте радиус-вектора" не изменяется так называемый квадрат интервала:
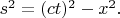
Если из этого равенства выразить

через

(если
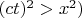
или

через

(если
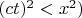
и построить графики получившихся зависимостей (при
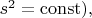
то это будут гиперболы. Когда будете подробно изучать учебники по СТО, легко в этом разберётесь, если потребуется.
Ну хорошо; полагаю, Вы на данном этапе разобрались в том, что хотели понять, так что угомоняюсь с этой темой :). Форумчане Вам помогали и ещё помогут, если что.