a^2+4a+4b=z^2

[juna]

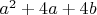
Для целых $a, b$ выражение $a^2+4a+4b$ должно быть точным квадратом. Для каждого $a$ можно найти серию таких $b$. В обследованных мной вариантах возможны три (четыре) случая:
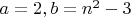
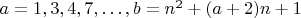
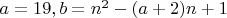
1. $a=2, b=n^2-3$
2. $a=1,3,4,7,\ldots , b=n^2+(a+2)n+1$, $a=19, b=n^2-(a+2)n+1 $
3. $a=5,6,8,9,10,11,12,13,14,15,16,17,18,\ldots , b=n^2+an-a$
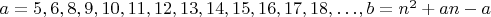
Не могу понять, как от значения $a$ зависит, какой формой для $b$ нужно воспользоваться, существуют ли другие формы?

[Dmitriy40]

Вольфрам показывает и много других, вроде бы ...

[waxtep]

Можно ведь написать $b=\ldots$, и тогда $a,z$ д.б. одинаковой четности

[worm2]

waxtep, ну да, рассмотреть два случая: чётных и нечётных $a$.
Если $a$ чётное, то и квадрат должен быть чётным: $a^2+4a+4b=(2n)^2$, откуда $b=n^2-a^2/4-a$
Если $a$ нечётное, то и квадрат должен быть чётным: $a^2+4a+4b=(2n+1)^2$, откуда $b=n^2+n-(a^2-1)/4-a$

[juna]

worm2 в сообщении #1703232 писал(а):

waxtep, ну да, рассмотреть два случая: чётных и нечётных $a$.
Если $a$ чётное, то и квадрат должен быть чётным: $a^2+4a+4b=(2n)^2$, откуда $b=n^2-a^2/4-a$
Если $a$ нечётное, то и квадрат должен быть чётным: $a^2+4a+4b=(2n+1)^2$, откуда $b=n^2+n-(a^2-1)/4-a$

Ах, спасибо. Про $z$ я вообще не задумывался, соответственно и четность прошла мимо. И на самом деле это просто сдвиг, например, для $a=19$, получаем $f(n)=b=n^2+n-109, f(n-11)=n^2-21n+1$