Найти предел последовательности, используя непрерывность

[Gecko]

Используя непрерывность соответствующей функции, вычислить предел последовательности $a_n = (1 + \frac{x_n}{n})^n$, если $\lim\limits_{n \to\infty} x_n = x \in \mathbb{R}$.
Понятно, что ответ будет $e^x$. Но я могу его получить, только если независимо устремляю к бесконечности $n$ для $x_n$ и $n$ в знаменателе и показателе степени. Но это как-то неправильно. Это же одна и та же $n$.

[GAA]

Нужно посмотреть в конспекте или рекомендованном учебнике определение степенно-показательной функции.
Если $u(x)^{v(x)}=e^{v(x)\ln u(x)}$, то все просто:
$\lim\limits_{n \to \infty} ( 1 + x_n/n)^n = \lim\limits_{n \to \infty} e^{n\ln(1+x_n/n)}$.
Предел аргумента экспоненты вычисляется легко, учитывая, что $x_n/n$ бесконечно малая функция:
$\lim\limits_{n \to \infty} n \ln(1+x_n/n) = \lim\limits_{n \to \infty} n x_n/n = \lim\limits_{n \to \infty} x_n = x$.
Используя непрерывность экспоненты, окончательно получаем
$\lim\limits_{n \to \infty} ( 1 + x_n/n)^n =e^x$.

[Gecko]

Всё понятно, спасибо!
Еще одна задачка из похожей серии.
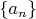
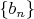
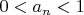
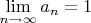
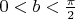
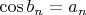
Последовательности $ \{a_n\} $ и $ \{b_n\} $ таковы, что $0 < a_n < 1$, $\lim\limits_{n \to\infty} a_n = 1$, $0 < b < \frac{\pi}{2}$, $\cos b_n = a_n$. Найти $\lim\limits_{n \to\infty}\frac{b_n}{\sqrt{1 - a_n}}$.

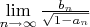
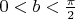
Косинус - непрерывная функция, поэтому можем написать, что $\lim\limits_{n \to\infty} a_n = \lim\limits_{n \to\infty} \cos b_n = \cos \lim\limits_{n \to\infty} b_n = 1$, откуда, с учетом того, что $0 < b < \frac{\pi}{2}$, получаем, что $\lim\limits_{n \to\infty} b_n = 0$.

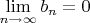
Далее, $\lim\limits_{b_n \to 0} \frac{b_n}{\sqrt{1 - \cos b_n}} = \lim\limits_{b_n \to 0} \frac{b_n}{\sqrt{2 \sin^2 b_n/2}} = \lim\limits_{b_n \to 0} \frac{2 b_n / 2}{\sqrt{2} \sin b_n/2} = \sqrt{2}$.

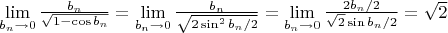
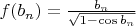
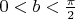
$f(b_n) = \frac{b_n}{\sqrt{1 - \cos b_n}}$ - непрерывная функция на интервале $0 < b < \frac{\pi}{2}$, значит $\lim\limits_{n \to \infty} \frac{b_n}{\sqrt{1 - a_n}} = \sqrt{2}$.

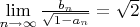
Хотелось бы понять, правильны ли мои рассуждения.

[Null]

Gecko в сообщении #1702601 писал(а):

$\lim\limits_{n \to\infty} \cos b_n = \cos \lim\limits_{n \to\infty} b_n $

В этом переходе требуется существование $\lim\limits_{n \to\infty} b_n$

[Gecko]

Ага, тогда попробуем так. Ввиду того, что функция $f(x) = \arccos x $ непрерывна на отрезке [-1, 1]:

$\lim\limits_{n \to\infty} b_n = \lim\limits_{n \to\infty}\arccos a_n = \arccos \lim\limits_{n \to\infty} a_n = \arccos 1 =0$.

[Gecko]

А вот еще один пример. Используя непрерывность соответствующей функции, найти предел последовательности $\left\lbrace \cos \frac{x}{2} \cos \frac{x}{2^2}...\cos \frac{x}{2^n}\right\rbrace$ при $x \ne 0$.

$\lim\limits_{n \to \infty} (\cos \frac{x}{2} \cos \frac{x}{2^2}...\cos \frac{x}{2^n}) = \lim\limits_{n \to \infty} \frac{\sin x}{2^n \sin \frac{x}{2^n}} = \frac{\sin x}{x} \lim\limits_{n \to \infty} \frac{\frac{x}{2^n}}{\sin \frac{x}{2^n}} = \frac{\sin x}{x}$.

Вот только не пойму, при чем здесь непрерывность функции.

[nnosipov]

Gecko в сообщении #1702871 писал(а):

Вот только не пойму, при чем здесь непрерывность функции.

Функция $\sin{x}/x$, доопределенная в нуле единицей, является непрерывной. Переходим к пределу под знаком непрерывной функции.

[Gecko]

Понятно, спасибо. А я думал, что $x$ - фиксированное число.

[Dedekind]

Gecko в сообщении #1702918 писал(а):

А я думал, что $x$ - фиксированное число.

Так это так и есть.

[Gecko]

Тогда не пойму, где именно переходим к пределу под знаком непрерывной функции.

[nnosipov]

Gecko в сообщении #1702925 писал(а):

Тогда не пойму, где именно переходим к пределу под знаком непрерывной функции.

Пардон, не ту функцию указал. В Вашем решении речь идет о функции $f(t)=t/\sin{t}$, доопределенной $1$ при $t=0$. Она непрерывна, поэтому

$$\lim_{n \to \infty}{f(t_n)}=f\left(\lim_{n \to \infty}{t_n}\right).$$

У Вас $t_n=x/2^n \to 0$.

[Gecko]

Ну в том-то и дело. Все-таки $f(t)$ имеет точку разрыва при $t = 0$. Получается, что $\lim\limits_{n \to \infty}f(t_n)=f( \lim\limits_{n \to \infty}t_n)$ выполняется не потому, что $f(t)$ непрерывна при $t = 0$, а потому, что существует окрестность нуля, где $t_{n} \ne 0$.

[Dedekind]

Gecko в сообщении #1702985 писал(а):

Все-таки $f(t)$ имеет точку разрыва при $t = 0$.

Нет. Если у Вас область определения $f(t)$ - это $R/\{0\}$, то в точке $t = 0$ функция попросту не определена. Это НЕ точка разрыва. А если вы по непрерывности доопределите на $R$: $f(t) = t/\sin t$, если $t\ne 0$ и $f(t) = 1$, если $t=0$, то тогда тем более $t = 0$ НЕ будет точкой разрыва. И тогда указанное равенство выполняется именно в силу непрерывности функции.
Если же доопределить функцию таким образом, чтобы $t=0$ действительно была точкой разрыва, то тогда равенство будет неверным.

[Gecko]

Dedekind в сообщении #1702986 писал(а):

Нет. Если у Вас область определения $f(t)$ - это $R/\{0\}$, то в точке $t = 0$ функция попросту не определена. Это НЕ точка разрыва.

А как же определение?
Пусть $f$ определена в $\dot{U}_\delta(t_0)$. Если $\exists \lim\limits_{t \to t_0} f(t) \in \mathbb{R}$, но в точке $t_0$ функция $f$ не определена либо $f(t_0) \ne \lim\limits_{t \to t_0}f(t)$, то точка $t_0$ называется точкой устранимого разрыва.

[Dedekind]

Gecko
Да, при таком определении - будет точкой разрыва.