Интуитивно-правдоподобные утверждения в общей топологии часто нетривиальным образом зависят либо от тонкостей аксиоматики типа ZFC, либо требуют для своей верности предположений теоретико-множественного характера. И, наоборот, порой довольно смелые утверждения не требуют каких бы то ни было предположений. Предлагаю делиться любопытными примерами такого рода. Вроде таких:
Утверждение 1. Если каждое открытое множество в метрическом пространстве является счетным объединением шаров, то такое пространство является
сепарабельным.Доказательство утверждения опирается на континуум-гипотезу. Правда, можно несколько ослабить условие, заменив континуум-гипотезу на предположение
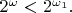 Утверждение 2.
Утверждение 2. Пусть
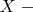 хаусдорфово пространство.
хаусдорфово пространство. Тогда компактность

равносильна:
1)
Линделёфовости 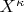
для любого кардинала

2) Линделёфовости
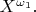
Упоминаемое здесь свойство по имени финского математика Эрнста Линделёфа - очень естественное свойство пространства в общей топологии (определение - по ссылке). Её прямая связь с компактностью довольно неожиданна, по крайней мере, для меня. Утверждение
доказуемо без привлечения каких-либо гипотез!
Я понимаю, что книга "Контрпримеры в топологии" напичкана такими примерами, но, во-первых, она не является исчерпывающей; к примеру, исходных утверждений там нет. Во-вторых, хотелось бы отобрать наиболее яркие утверждения, которые, может быть, удивили лично Вас или даже поменяли Ваше представление о метрических и топологических пространствах.
-- 16.09.2025, 07:21 --Утверждение 3. Существует непрерывная (!) сюръекция из множества иррациональных чисел

с унаследованной из

топологией в
 Доказательство.
Доказательство. Пусть

есть действительное число с целой частью как у

и у которого каждая

-ая цифра после запятой совпадает с

цифрой исходного

Например, число

этой функцией отображается следующим образом:
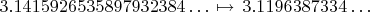
Эта функция сюрьективна, так как цифры любого действительного

можно чередовать с любым нецикличным паттерном, а потому
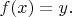
Также она непрерывна, потому что из

следует
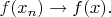
В доказательстве есть даже большой произвол: вместо
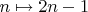
можно выбирать другие правила; на самом деле, можно оставлять какие угодно бесконечные последовательности цифр после запятой.