Сейчас еще раз проверил, там написано именно
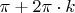
- точка локального максимума.
В учебнике ошибка. Постройте график исходной функции

на компьютере и убедитесь, что например

там точка минимума. Как у Вас изначально и получилось.
Получается, нужно для промежутка корней с наибольшей серией рассмотреть также все корни из серии, период которой меньше?
Тут важно не то, что
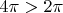
, а то, что

делится на

. Вы же сами сказали, что на любом промежутке длины

есть два корня из серии

. Два корня - это потому что

.
То есть в данном случае нужно рассмотреть:
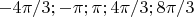
?
Может Вы и правы, но я не знаю, что Вы имеете в виду, когда говорите "нужно рассмотреть". Я бы сказал так. Вся числовая прямая разбивается на промежутки длины

: это промежутки
![$\ldots,\,[-4\pi,0],\,[0,4\pi],\,[4\pi,8\pi],\,\ldots$ $\ldots,\,[-4\pi,0],\,[0,4\pi],\,[4\pi,8\pi],\,\ldots$](https://dxdy-04.korotkov.co.uk/f/7/1/2/712011d89985eae69f5dd39238a096f882.png)
- то есть на промежутки вида
![$[4\pi k,4\pi(k+1)]$ $[4\pi k,4\pi(k+1)]$](https://dxdy-02.korotkov.co.uk/f/5/9/e/59e1d44c31192c40607927244b30fb4e82.png)
, где

целое. Вот и напишите, какие корни будут на произвольном промежутке
![$[4\pi k,4\pi(k+1)]$ $[4\pi k,4\pi(k+1)]$](https://dxdy-02.korotkov.co.uk/f/5/9/e/59e1d44c31192c40607927244b30fb4e82.png)
. Если хотите, можете выписать корни на промежутке
![$[0,4\pi]$ $[0,4\pi]$](https://dxdy-04.korotkov.co.uk/f/7/f/0/7f0e4997421cda9e2bf711a338b347d382.png)
, а затем прибавить к ним произвольное

.
Почему рассматриваем именно отрезки длины

? Потому что

делится на периоды каждой серии корней. Например, если бы были серии корней с
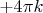
и c
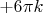
, надо было бы рассматривать промежуток длины

- на каждом таком промежутке было бы три корня из серии с
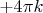
и два корня из серии с
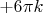
.