Зависимости в кортежах простых чисел

[vicvolf]

Гипотеза Харди-Литтлвуда и модель Крамера
Гипотеза Харди-Литтлвуда утверждает, что количество простых $k$-кортежей с шаблоном $H$ до $x$ асимптотически равно:
$\pi_H(x) \sim C(H) \cdot \frac{x}{(\ln x)^k},$
где $C(H)$ — константа, зависящая от шаблона $H$.

В модели Крамера предполагается, что события "число $n$ простое" независимы для разных $n$, и вероятность того, что $n$ простое, равна $1/\ln n$. Если бы эта модель была точной, то вероятность того, что все $k$ чисел в кортеже простые, была бы произведением вероятностей:
$P(n, n+d_1, \ldots, n+d_{k-1} \text{ простые}) \approx \frac{1}{\ln n} \cdot \frac{1}{\ln (n+d_1)} \cdot \ldots \cdot \frac{1}{\ln (n+d_{k-1})} \approx \frac{1}{(\ln x)^k}.$
Тогда ожидаемое количество кортежей до $x$ было бы:
$\pi_H(x) \sim \frac{x}{(\ln x)^k},$
то есть для независимой модели $C(H) = 1$.

Почему в гипотезе Харди-Литтлвуда $C(H) \neq 1$?
На самом деле, модель Крамера является упрощенной и не учитывает два важных аспекта:
1. Четность простых чисел: Все простые числа, кроме 2, нечетные. Поэтому для кортежей с четными разностями (что обычно и рассматривается) все числа в кортеже нечетные. Вероятность того, что случайное нечетное число простое, примерно равна $2/\ln x$ (поскольку половина чисел нечетные). Если в модели независимости учесть это, то вероятность того, что все $k$ чисел простые, становится:
$ \left( \frac{2}{\ln x} \right)^k. $
Тогда ожидаемое количество кортежей (учитывая, что примерно половина чисел нечетные) будет:
$ \pi_H(x) \sim \frac{x}{2} \cdot \left( \frac{2}{\ln x} \right)^k = 2^{k-1} \cdot \frac{x}{(\ln x)^k}. $
Таким образом, в этой скорректированной независимой модели $C(H) = 2^{k-1}$.

2. Влияние малых простых чисел: В реальности простые числа не полностью независимы — их распределение имеет корреляции из-за деления на малые простые числа. Гипотеза Харди-Литтлвуда учитывает это через константу:
$ C(H) = 2^{k-1} \cdot \prod_{p > 2} \frac{1 - \frac{\nu_H(p)}{p}}{(1 - \frac{1}{p})^k}, $
где $\nu_H(p)$ — количество различных остатков по модулю $p$ в кортеже $H$. Это отражает поправки на то, что числа в кортеже избегают общих делителей с малыми простыми.

Таким образом, коэффициент $C(H)$ отражает зависимость простых чисел в кортеже.

Рассмотрим случай, когда длина кортежа $k=2$. Паттерн (шаблон) данного кортежа имеет вид $(0,d)$, где $d$ - диаметр кортежа.

Допустимость кортежей вида $ (0, d) $
Кортеж $ H = (0, d) $ всегда является допустимым для любого $ d $. Это означает, что для любого простого числа $ p $ остатки элементов кортежа по модулю $ p $ не покрывают все множество вычетов $ \{0, 1, \dots, p-1\} $.

- Для $ p = 2 $:
- Элементы: $ 0 $ и $ d $.
- Остатки: $ 0 \mod 2 = 0 $, $ d \mod 2 $ зависит от четности $ d $.
- Если $ d $ четное, остатки: $ \{0\} $, что не покрывает $ \mathbb{Z}_2 = \{0, 1\} $.
- Если $ d $ нечетное, остатки: $ \{0, 1\} $, но кортеж $ (0, d) $ не может состоять из простых чисел, так как $ 0 $ не является простым. На практике рассматриваются только четные $ d $, поэтому остатки всегда $ \{0\} $.

- Для $ p > 2 $:
- Если $ p \mid d $, остатки: $ 0 $ и $ 0 $, то есть $ \{0\} $, что не покрывает $ \mathbb{Z}_p $.
- Если $ p \nmid d $, остатки: $ 0 $ и $ d \mod p \neq 0 $, то есть два различных остатка, но $ p \geq 3 $, поэтому они не покрывают все $ p $ вычетов.

[vicvolf]

Создается впечатление, что при $d \to \infty$, зависимость между простыми в кортеже должна уменьшаться и $C(H) \to 1$.
Однако, это не так. При некоторых последовательностях $d(n)$, при $n \to \infty$ ,значение $ C(H) \to \infty$. При других последовательностях $d(n)$, при $n \to \infty$ , значение $C(H)$ не меняется. Покажем это.

Для кортежа $ H = (0, d) $ постоянная Харди-Литтлвуда рассчитывается по формуле для пар простых чисел ($k=2$):

$$C(H) = 2 \cdot \prod_{p>2} \frac{1 - \frac{\nu_H(p)}{p}}{(1 - \frac{1}{p})^2},$$

где $\nu_H(p)$ — количество различных остатков элементов кортежа по модулю $p$.

Для $H = (0, d)$:
- Простые делители d (кроме 2): $p = 3$ , $p = 5$,…,$p \leq d$.
- Для $p|d$: остатки совпадают ($\nu_H(p) = 1$).
- Для остальных $p > 2$: остатки различны ($\nu_H(p) = 2$).

Поэтому постоянная упрощается до:

$$C(H) = 2C_2 \cdot \prod_{\substack{p > 2 \\ p \mid d}} \frac{p-1}{p-2},(1)$$

где $C_2 \approx 0.66016181584686957$ — постоянная простых близнецов.

Обзор предела константы Харди-Литтлвуда для кортежей вида $ H = (0, d(n)) $ при $ n \to \infty $

1. Последовательности с ограниченными простыми делителями
Если все $ d(n) $ имеют только фиксированное множество простых делителей, то произведение в формуле (1) для $ C(H) $ ограничено, и предел конечен.

- Пример: $ d(n) = 2^n $.
- Простые делители: только 2 (учитывается в множителе 2).
- Тогда $ C(H) = 2C_2 \cdot 1 = 2C_2 \approx 1.32032$.
- Предел: $ \lim_{n \to \infty} C(H) = 2C_2 \approx 1.32032 $. (2)

2. Последовательности с простыми делителями, растущими достаточно быстро
Если простые делители $ d(n) $ растут так быстро, что ряд $\sum \frac{1}{p} $ сходится, то произведение сходится к конечному пределу.

- Пример: $ d(n) = p_n $ (n-е простое число).
- Для каждого $ d(n) $ есть только один простой делитель $ p_n $ (кроме 2).
- Множитель в (1): $ \frac{p_n-1}{p_n-2} \to 1 $ при $ p_n \to \infty $.
- Тогда $ C(H) \to 2C_2 \approx 1.32032 $.(3)

[vicvolf]

3. Последовательности с растущим количеством малых простых делителей
Если $ d(n) $ включает все больше малых простых чисел, то произведение расходится, и $ C(H) \to \infty $.

- Пример: $ d(n) = q_n\# $ (праймориал, произведение первых $ n $ простых чисел).
- Используется асимптотика: $ \prod_{\substack{p > 2 \\ p \leq q}} \frac{p-1}{p-2} \sim 2C_2 \ln q $.
- Тогда, на основании (1), $ C(H) \sim 2C_2 \cdot (2C_2 \ln q) = 4C_2^2 \ln q $.
- Предел: $ \lim_{n \to \infty} C(H) = \infty $ (4).

Следовательно, в этом случае, зависимость между простыми в кортеже неограниченно возрастает.

4. Последовательности с умеренным ростом простых делителей
Если $ d(n) $ имеет простые делители, растущие как $ n $, то $ C(H) $ может колебаться или расти медленно.

- Пример: $ d(n) = n $.
- Значение $ C(H) $ зависит от количества и размера простых делителей $ n $.
- Если $ n $ имеет много малых простых делителей, $ C(H) $ может быть большим.
- Если $ n $ — простое число, $ C(H) \approx 2C_2 $.
- Единого предела нет, поведение неустойчиво.

Обратим внимание, что во всех рассмотренных случаях $d(n) \to \infty$ при $n \to \infty$.
Таким образом, на основании (2). (3). (4) постоянная $ C(H) $ для паттерна $(0,d(n))$ может сходиться к $ 2C_2 $, расходиться к бесконечности или колебаться в зависимости от арифметических свойств $ d(n) $.
Аналогично себя ведет зависимость между простыми, в соответствующих паттерну $(0,d(n))$ кортежах, при $d(n) \to \infty$.

[vicvolf]

Теперь рассмотрим случай симметричных простых кортежей.

Определение симметричного простого кортежа
Симметричный простой кортеж длины $ k $ с диаметром $d $ имеет паттерн:
$H = (0, a_1, a_2, \ldots, a_{k-1}) \quad \text{с условием} \quad a_i + a_{k-i} = d.$
Это означает, что элементы кортежа, состоящего из простых чисел, симметрично распределены относительно центра.

Доказательство уменьшения постоянной Харди-Литтлвуда $C(H)$ для симметричных простых кортежей при уменьшении плотности паттерна

Рассмотрим поведение постоянной Харди-Литтлвуда $C(H)$ для симметричных простых кортежей при уменьшении плотности паттерна (уменьшении k при фиксированном $d$).

Константа Харди-Литтлвуда вычисляется по формуле:
$C(H) = \prod_{p} \frac{1 - \frac{\nu_H(p)}{p}}{(1 - \frac{1}{p})^k}$ (5)
где:
- $k$ - длина кортежа
- $\nu_H(p)$ - количество уникальных остатков элементов кортежа по модулю $p$

Влияние уменьшения $k$

При уменьшении $k$ (уменьшении плотности паттерна) при фиксированном диаметре $d$ в формуле (5) происходят два основных изменения:
a) Изменение знаменателя
Знаменатель $(1 - \frac{1}{p})^k$ уменьшается с уменьшением $k$, что стремится увеличить значение каждого множителя.
b) Изменение числителя
Числитель $1 - \frac{\nu_H(p)}{p}$ изменяется в зависимости от изменения $\nu_H(p)$. При удалении элементов из паттерна:
- $\nu_H(p)$ может уменьшиться (если удаляются элементы с уникальными остатками)
- $\nu_H(p)$ может остаться неизменным (если удаляются элементы с неуникальными остатками)

Комбинированный эффект
Для анализа общего эффекта рассмотрим отношение $C(H)$ для двух последовательных паттернов на основании (5):

$\frac{C(H_k)}{C(H_{k-1})} = \prod_{p} \frac{1 - \frac{\nu_{H_k}(p)}{p}}{1 - \frac{\nu_{H_{k-1}}(p)}{p}} \cdot \frac{1}{1 - \frac{1}{p}}$. (6)

Для симметричных кортежей с большим диаметром выполняется:
- $\nu_{H_k}(p) \approx k$ для большинства $p$
- $\nu_{H_{k-1}}(p) \approx k-1$ для большинства $p$

Поведение остатков по модулю больших простых чисел ($ p > d $)
- Для любого простого $ p > d $ все элементы кортежа лежат в интервале $ [0, d] \subset [0, p) $.
- Поскольку все элементы различны, их остатки по модулю $ p $ также различны.
- Следовательно, для всех $ p > d $ выполняется:
$ \nu_{H_k}(p) = k, \quad \nu_{H_{k-1}}(p) = k-1.$
- Это точное равенство (не приближение).

Тогда. на основании (6):
$\frac{C(H_k)}{C(H_{k-1})} \approx \prod_{p} \frac{1 - \frac{k}{p}}{1 - \frac{k-1}{p}} \cdot \frac{1}{1 - \frac{1}{p}} = \prod_{p} \frac{p-k}{p-k+1} \cdot \frac{p}{p-1}$. (7)

Отношение (7) меньше 1 для $k > 2$, что подтверждает убывание $C(H)$ с уменьшением $k$.
Таким образом, для симметричных простых кортежей, зависимость между простыми в кортеже уменьшается с убыванием плотности паттерна.

[vicvolf]

В качестве примера рассмотрим симметричные кортежи с паттерном $k=17,d=240$.

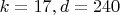
Я уже определял для этого случая значения постоянных Харди-Литтлвуда $C(H)$ по мере уменьшения плотности паттерна здесь.

На основании предоставленных данных составлена следующая таблица, показывающая изменение константы Харди-Литтлвуда $C(H)$ при уменьшении длины кортежа $k$ (уменьшении плотности паттерна):

| Длина кортежа ($k$) | Паттерн | $C(H)$ | Отношение $C(H_{k-2})/C(H_{k}) $|

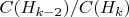
| 17 | [0, 6, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 234, 240]| 2.0427×10⁸ | - |
| 15 | [0, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 240] | 1.5265×10⁷ | 0.0747 |
| 13 | [0, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 240] | 1.6893×10⁶ | 0.1107 |
| 11 | [0, 66, 84, 90, 114, 120, 126, 150, 156, 174, 240] | 1.1665×10⁵ | 0.0691 |
| 9 | [0, 84, 90, 114, 120, 126, 150, 156, 240] | 9.6778×10³ | 0.0830 |
| 7 | [0, 90, 114, 120, 126, 150, 240] | 5.0374×10² | 0.0521 |
| 5 | [0, 114, 120, 126, 240] | 9.2634×10¹ | 0.1839 |
| 3 | [0, 120, 240] | 1.1433×10¹ | 0.1234 |
| 2 | [0, 240] | 3.5209×10⁰ | 0.3079 |

Выводы:

1. Монотонное уменьшение $C(H)$: При уменьшении длины кортежа k значение константы C(H) последовательно уменьшается, что подтверждает ослабление зависимости между простыми числами в кортеже.

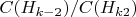
2. Отношения $C(H_{k-2})/C(H_{k2})$: Все вычисленные отношения меньше 1, что свидетельствует о том, что уменьшение $C(H)$ происходит быстрее, чем линейное.

3. С уменьшением плотности кортежа (уменьшением $k$) значение $C(H)$ приближается к минимальному значению, что соответствует ослаблению зависимости между простыми числами в кортеже.

Данная таблица наглядно демонстрирует, что с уменьшением плотности паттерна (уменьшением количества элементов в кортеже) постоянная Харди-Литтлвуда $C(H)$ монотонно уменьшается, что согласуется с теоретическими ожиданиями об ослаблении зависимости между простыми числами в "рыхлых" кортежах.