Тогда
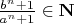
при всех

. Согласно известной задаче (на этом форуме этот сюжет несколько раз всплывал, ссылки искать лень)
О, да) Только, насколько я помню, речь там шла о дроби
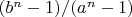
. Мне тоже ссылку искать лень, но я укажу на первоисточник (вероятно) этой задачи: Cavachi M. A Powerful Property // Amer. Math. Monthly. 2000. Vol. 107. № 7. P. 654. Что забавно: с этой задачей никто из читателей AMM тогда не справился, и было опубликовано решение by the proposer (на мой взгляд, несколько искусственное, на dxdy решения были более идейные).