Коллеги, не знает ли кто-нибудь ответа на следующий вопрос?
Даны два многочлена
![$f(x,y), g(x,y)\in{\mathbb Z}[x,y]$ $f(x,y), g(x,y)\in{\mathbb Z}[x,y]$](https://dxdy-02.korotkov.co.uk/f/5/0/d/50d09c5d63a9ce79ca887f523e0742cc82.png)
,

,

, и
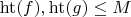
(высота --- максимум модуля коэффициентов). Надо найти многочлен
![$q\in{\mathbb Z}[x]$ $q\in{\mathbb Z}[x]$](https://dxdy-02.korotkov.co.uk/f/5/8/e/58e5724b423b2b820e19ae179b6514f982.png)
такой, что

для любого решения системы
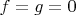
(т.е. исключить неизвестную

). Какова сложность (точнее, известная верхняя оценка на битовую сложность) этой задачи ? Написать конкретную функцию от
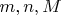
. Что это: многочлен, экспонента, двойная экспонента ?