Спасибо, но огорчили. Для моей исходной задачи нужно было получить все рациональные решения приведенного уравнения.
Например, как у Вас, для произвольного m. Пытаясь уйти от эллиптической кривой, рассматриваю Ваше представление исходного уравнения как гиперболу на плоскости
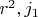
. Там, кроме Ваших рациональных точек при
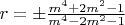
, есть еще при
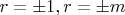
.
Авось удастся все найти?
-- 17.08.2025, 14:50 --Грок меня обнадежил относительно эллиптических кривых. Оказывается что существуют семейсва таких однопараметрических кривых, с постоянным рангом для всех кривых семейсва! Если бы у кривых
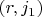
в Вашем представлении это было справедливо для произвольных допустимых m, и ранг был 1, это решило бы мою задачу.
Но мне врядли по силам провести такой анализ!