Области определения корней и дробных степеней различаются?

[Charlz_Klug]

Вычитал вот такое:

Цитата:

В нечётном случае области определения корней и дробных степеней различаются. Например, область определения $\sqrt[3]{x}$ — все действительные числа, а область определения $x^{1/3}$ — все неотрицательные числа.

Как это так? Почему я не могу в $x^{1/3}$ подставить $-1$ например?

[wrest]

Charlz_Klug в сообщении #1696953 писал(а):

Как это так? Почему я не могу в $x^{1/3}$ подставить $-1$ например?

Потому что $\sqrt[3]{x}$ и $x^{1/3}$ разные функции, по некоему соглашению.
См. например «Корень vs. степень: область определения»

[Mikhail_K]

Charlz_Klug в сообщении #1696953 писал(а):

Почему я не могу в $x^{1/3}$ подставить $-1$ например?

Это соглашение. То есть в одних математических книгах может быть написано, что можете, а в других - что не можете.

Примерно как в одних математических книгах $0$ считается натуральным числом, а в других не считается. Это не какая-то истина, а вопрос удобства.

Мне кажется более удобным считать, что отрицательные числа нельзя возводить в дробные степени - и, таким образом, $\sqrt[3]{-1}=-1$, но $(-1)^{1/3}$ не существует. Если, конечно, речь не идёт о комплексных числах - комплексная степень это отдельный разговор.

Вот почему это удобно. Во-первых, чтобы не получалось парадоксов вроде $-1=\sqrt[3]{-1}=(-1)^{1/3}=(-1)^{2/6}=\sqrt[6]{(-1)^2}=\sqrt[6]{1}=1$. Тут можно, конечно, наложить запрет на переходы типа $(-1)^{2/6}=\sqrt[6]{(-1)^2}$, разрешив делать такие переходы только с несократимыми дробями в показателе - но это слишком сложно и вряд ли нужно. Проще запретить дробные степени отрицательного аргумента.

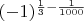
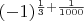
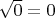
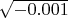
Во-вторых, очень странно выглядит, когда $(-1)^{\frac{1}{3}}$ существует, а $(-1)^{\frac{1}{3}-\frac{1}{1000}}$ и $(-1)^{\frac{1}{3}+\frac{1}{1000}}$ не существуют. От арифметических действий ожидаешь, что небольшие изменения аргументов не должны существенно портить результат. Конечно, для обычных корней тоже можно указать что-то чуть-чуть похожее: $\sqrt{0}=0$, но $\sqrt{-0.001}$ не существует - но в случае с дробными степенями отрицательных чисел всё выглядит значительно хуже. Начнёшь изменять показатель степени, а результат сразу станет часто мелькать - то существует, то не существует. Некрасиво.