amonЭто все, конечно, окончательно меня запутало, поскольку и во многих статьях вводится, как вы говорите, взаимодействие света со светом. Давайте я уточню, что у меня за система. Она состоит из:
1) Резонатора с двумя модами. Первая на половине частоты перехода
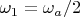
, ее энергия
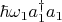
, вторая на частоте перехода

.
2) Атома (пока одного):
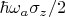
3) Взаимодействия между ними вида
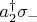
(однофотонное взаимодействие на частоте перехода), и
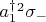
(двухфотонное возбуждение атома).
При этом мой резонатор накачивается лазером на

(

). Тогда возникает вопрос, как правильно записать гамильтониан. Можем тогда считать поле на

классическим, а вот поле на частоте перехода остается квантовым. Правильно ли я понимаю, что в Ваших обозначениях гамильтониан примерно такой:
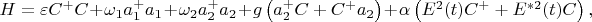
?
Потери я учту через взаимодействие с резервуаром и линдбладиан. Если я вас правильно понял, то как в таком случае связаны

и
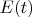
? В уравнении Гейзенберга для оператора

будет справа сидеть

, а уравнение для C в свою очередь будет справа у себя содержать

. То есть связь

c полем накачки получается неявная, через уравнение Гейзенберга для
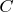
?