Заголовок кликбейт
Помогите, пожалуйста, разобраться.
Открыл Зорича 1 часть, читаю 8 страницу гл.1 "некоторые общематематические понятия и обозначения"
Автор доказывает формулы де-моргана.
У меня возникло 2 вопроса касательно примера с этой страницы. Пример выглядит следующим образом:
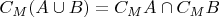
1) Почему он доказывает одну формулу дважды (от "необходимого" условия и от "достаточного"), если он уже получил из левой части формулы выражение, равносильное правой?
2) А с чего автор решил, что из того, что
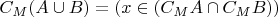
следует, что
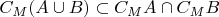
?