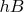Геометрия - сравнение площадей фигур

[Ilya83]

Всем здравствуйте! При решении задачи для 8 кл. по геометрии, появилось смущение.

Задача:

Цитата:

Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника.

Цитата:

Параллелограмм — четырёхугольник, у которого противолежащие стороны попарно параллельны

Цитата:

Прямоугольник — четырёхугольник, у которого все углы прямые

Площадь прямоугольника S=AB
Площадь параллелограмма S=hB

Если взять прямоугольник с известными сторонами hB и начать превращать его в параллелограмм, то получится, что h, как высота, а следовательно и площадь фигуры начнет изменяться.

Но при этом стороны h и B не изменяются. Меняются только углы. Т.е. уравнение S=hB не изменяется.

Как же получается, что площадь изменяется
Спасибо.

[slavav]

$h$ не сторона параллелограмма, а его высота. И она зависит от углов.

[wrest]

Ilya83
Был прямоугольник площадью S, а потом его "пригнули" так что стороны остались те же, а площадь уменьшилась в два раза.

Ну вы правильно заметили, что когда прямоугольник сплюснулся, его высота уменьшилась, значит, в два раза. На какой угол надо отклонить вертикальную палку чтобы её высота уменьшилась в два раза? Какой тогда угол палка составит с горизонталью?
По идее, задача устная...

[Ilya83]

wrest
Вы соглашаетесь с формулой вычисления площади S=hB и при этом обращаете внимание на изменившийся угол (что отображено на Вашем рисунке).
Не значит ли это, что в формуле вычисления площади чего-то не хватает?

Если я возьму веревку, свяжу в узилок и растяну в высоту, я получу, допустим, h=10, B=1. Если затем я эту же петлю растяну в ширину, я получу h=1, B=10. Площадь фигуры при этом не изменится. Почему? Не изменился угол?

[Booker48]

Ilya83 в сообщении #1695463 писал(а):

Не значит ли это, что в формуле вычисления площади чего-то не хватает?

Не хватает понимания, что такое $h$ в формуле площади параллелограмма. И про это slavav уже написал выше.

[Ilya83]

slavav
Вы тоже указали на углы.

Если я возьму петлю в виде фигуры треугольник, то изменение высоты не изменит площадь никак, т.к. при изменении высоты у меня будет меняться основание. Т.е. будет зависимость основания от высоты.

[slavav]

$h = A\sin\alpha$, где $A$ - сторона паралеллограмма, $\alpha$ - угол между сторонами $A$ и $B$.

[wrest]

Ilya83 в сообщении #1695463 писал(а):

Вы соглашаетесь с формулой вычисления площади S=hB и при этом обращаете внимание на изменившийся угол (что отображено на Вашем рисунке).
Не значит ли это, что в формуле вычисления площади чего-то не хватает?

Не хватает вашего понимания формулы (что в ней обозначают буквы).
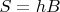
Формула $S=hB$ одинаково справедлива для всех параллелограммов, в том числе и для прямоугольников, ромбов, квадратов.
В этой формуле $B$ -- какая-то из сторон, а $h$ -- высота, проведенная к $B$. Высота здесь -- это расстояние от прямой, содержащей сторону $B$ до [параллельной ей] прямой, содержащей противолежащую стороне $B$ сторону). В случае прямоугольника, высота просто равна смежной с $B$ стороне, т.е. $h=A$
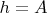
Если вы посмотрите на мой рисунок в моём предыдущем посте ещё раз, то увидите, что я обозначил высоты прямоугольника и параллелограмма как $h$ и $h/2$ соответственно.
Смотрите, вот два параллелограмма

У них одна и та же высота и равны стороны, к которым проведена (на которые опущена) высота.
Их площади равны. А углы, и стороны смежные с $B$ -- не равны.

-- 26.07.2025, 22:39 --

Ilya83 в сообщении #1695463 писал(а):

я получу, допустим, h=10, B=1. Если затем я эту же петлю растяну в ширину, я получу h=1, B=10. Площадь фигуры при этом не изменится. Почему? Не изменился угол?

Очевидно, потому, что не изменилось произведение $hB$

[Ilya83]

wrest

Цитата:

Очевидно, потому, что не изменилось произведение $hB$

Очевидно, что ни площадь, ни объем не могут уменьшиться при изменении формы фигуры.

Если я возьму шарик и залью в него 1л воды. Потом я могу придать этому шарику форму куба или тетраэдра. Но там как был 1л воды так и остался.

[Booker48]

Ilya83
Это неправильная аналогия. У вас неизменным является только периметр прямоугольника/параллелограмма.
Максимальная площадь из фигур равного периметра - у окружности (круга), минимальная равна 0.

[wrest]

Ilya83 в сообщении #1695493 писал(а):

Очевидно, что ни площадь, ни объем не могут уменьшиться при изменении формы фигуры.

Что бы это значило...

[Geen]

Ilya83 в сообщении #1695468 писал(а):

Если я возьму петлю в виде фигуры треугольник, то изменение высоты не изменит площадь никак, т.к. при изменении высоты у меня будет меняться основание.

А площадь изменится. Предельный случай - высота 0.

[Ilya83]

Цитата:

Предельный случай - высота 0

Нонсенс.

Если принять то, что у фигуры $h=0$, то используя $S=hB$, вся фигура обратится в 0. Фигура занимает площадь 0, т.е она исчезла. Но это невозможно, т.к. у фигуры есть основание $B\neq0$, которое занимает какое-то пространство.

[sergey zhukov]

Ilya83 в сообщении #1695493 писал(а):

Очевидно, что ни площадь, ни объем не могут уменьшиться при изменении формы фигуры.

Ничего себе, очевидное заявление. Очевидно-то как раз обратное. Вот я беру открытую пастиковую бутылку лимонада и сдавливаю ее руками. Площадь поверхности не меняется, а лимонад из горлышка начинает вытекать. Что же с объемом происходит?

-- 27.07.2025, 09:47 --

Ilya83 в сообщении #1695463 писал(а):

Если я возьму веревку, свяжу в узилок и растяну в высоту, я получу, допустим, h=10, B=1. Если затем я эту же петлю растяну в ширину, я получу h=1, B=10. Площадь фигуры при этом не изменится. Почему? Не изменился угол?

А если, допустим, квадрат из нее сделать с стороной 11/2? Как там с площадью? Не изменится? Это к тому, что там у вас случайное совпадение, из которого никакого вывода не следует про площадь фигуры, ограниченной ниткой фиксированной длины.

[wrest]

Ilya83 в сообщении #1695513 писал(а):

Если принять то, что у фигуры $h=0$, то используя $S=hB$, вся фигура обратится в 0.

Ну нет, не вся. А только её высота, площадь и пара углов (а ещё пара углов станут развёрнутыми). Если высота параллелограмма равна нулю, при том что основание не равно нулю, то получается, что праллелограмм выродился и превратился в отрезок.
Вот отрезок есть, а площади у него нет. Парадокс же, да?
Или вот возьмём какую-нибудь прямую. Прямая даже не имеет концов, верно? То есть -- бесконечна. Но какие же тогда у неё площадь и объем?