Геометрия - сравнение площадей фигур

[Лукомор]

Ilya83 в сообщении #1695447 писал(а):

Площадь прямоугольника S=AB
Площадь параллелограмма S=hB

Если взять прямоугольник с известными сторонами hB и начать превращать его в параллелограмм, то получится, что h, как высота, а следовательно и площадь фигуры начнет изменяться.

Но при этом стороны h и B не изменяются. Меняются только углы. Т.е. уравнение S=hB не изменяется.

Ошибка в том, что Вы одной и той же буквой $h$
обозначили и сторону квадрата, которая не изменяется при преобразовании квадрата в параллелограмм, и высоту параллелограмма, которая уменьшается при уменьшении угла между смежными сторонами параллелограмма.

Если взять прямоугольник с известными сторонами $AB$ и начать превращать его в параллелограмм, то получится, что $h$, как высота, а следовательно и площадь фигуры начнет изменяться.
Но при этом стороны $A$ и $B$ не изменяются. Меняются только углы. Т.е. уравнение $S=AB$ не изменяется, но это уравнение не является уравнением площади параллелограмма.
А в уравнении площади параллелограмма $S=hB$ высота параллелограмма
уменьшается при уменьшении угла между смежными сторонами параллелограмма.

[Ilya83]

Цитата:

Вот я беру открытую пастиковую бутылку лимонада и сдавливаю ее руками.

Тут ключевое слово открытую.

Я говорю о геометрической фигуре, рассматривая ее, как замкнутый контур.
Можно взять для примера тот самый египетский треугольник.

Цитата:

...то получается, что праллелограмм выродился и превратился в отрезок.

Я взял лист бумаги (у которого есть площадь) и начертил на нем отрезок (который ТОЖЕ занимает, какую-то площадь). Если потратить немного времени и начертить много таких отрезков, то в результате весь лист бумаги (вся его площадь) будет покрыта отрезками. Мы получили сложение площадей отрезков (по Вашим утверждениям, с нулевой высотой), которые в сумме равны площади листа бумаги... Парадокс

[Booker48]

Ilya83 в сообщении #1695534 писал(а):

...отрезок (который ТОЖЕ занимает, какую-то площадь)

Понятно. Вам нужно для начала понять, что такое геометрия.

[dgwuqtj]

Ilya83 в сообщении #1695534 писал(а):

Если потратить немного времени и начертить много таких отрезков, то в результате весь лист бумаги (вся его площадь) будет покрыта отрезками.

Вот поэтому (в том числе) рисунки на бумаге не являются математическими объектами и с их помощью ничего не доказывают. Они только для наглядности.

То есть математические отрезки (параллелограммы, точки и т.д.) и ваши картинки — это совсем разные вещи.

[sergey zhukov]

Ilya83
Парадокс - это когда человек о геометрии рассуждает, а не может даже понять, что на рисунке нарисовано, где площадь, где периметр, где угол. Хотя ему все это добрые люди нарисовали. И вместо этого начинает чепуху рассказывать о какой-то толщине линий.

[wrest]

Ilya83 в сообщении #1695534 писал(а):

Я взял лист бумаги (у которого есть площадь) и начертил на нем отрезок (который ТОЖЕ занимает, какую-то площадь).

А... Ну тут надо начинать повторение более ранних классов. В геометрии точки считают тем, у чего нет никакого размера, а толщину отрезков и прямых считают равной нулю. Если вы с этим не согласны/не понимаете/выражаете решительный протест ибо это противоречит здравому смыслу и жизненному опыту -- не решайте больше геометрических задач.
Впрочем, Готфрид Лейбниц вот тоже считал, что у всего есть хоть какой-то размерчишко, и в итоге изобрёл дифференциальное исчисление. Затем ещё явился Джузеппе Пеано и вот он почти что как вы -- зачертил квадрат линиями нулевой толщины так, что между ними уж решительно ничего просунуть было нельзя, сплошняком изрисовал, чем немало удивил сообщество. Может, и у вас что-нибудь этакое выйдет.

[Ilya83]

dgwuqtj
Я на это уже указал (см. выше)

Цитата:

Нонсенс.

Если принять то, что у фигуры $h=0$, то используя $S=hB$, вся фигура обратится в 0. Фигура занимает площадь 0, т.е она исчезла. Но это невозможно, т.к. у фигуры есть основание $B\neq0$, которое занимает какое-то пространство.

По Вашему получается, что фигура (с площадью) превратиться в отрезок (а отрезок - понятие абстрактное), т.е. фигура должна (по математической модели) исчезнуть. Я правильно Вас понял ?

[Booker48]

Ilya83 в сообщении #1695543 писал(а):

По Вашему получается, что фигура (с площадью) превратиться в отрезок (а отрезок - понятие абстрактное), т.е. фигура должна (по математической модели) исчезнуть. Я правильно Вас понял ?

Фигура трансформируется в отрезок, почему вы используете глагол "исчезнуть"?
А её площадь да, станет равной 0.

[wrest]

Ilya83 в сообщении #1695543 писал(а):

По Вашему получается, что фигура (с площадью) превратиться в отрезок (а отрезок - понятие абстрактное), т.е. фигура должна (по математической модели) исчезнуть.

Должна, но не исчезнуть, а выродиться в отрезок.
Вот смотрите. Берем три точки на какой-то одной прямой и соединяем их попарно в трегольник. Треугольник получился? Получился, но немножко ... дефективный: с нулевой площадью. Такие называют вырожденными треугольниками. Поищите в словаре. Ну или вот это гляньте: Вырождение

[provincialka]

Ilya83 в сообщении #1695543 писал(а):

По Вашему получается, что фигура (с площадью) превратиться в отрезок (а отрезок - понятие абстрактное), т.е. фигура должна (по математической модели) исчезнуть. Я правильно Вас понял ?

Так "геометрическая фигура" -- тоже вполне абстрактное понятие. И почему "исчезнуть"? Разве отрезок -- это "ничто"? Отрезок -- это вырожденный паралеллограмм (треугольник, многоугольник) и т.п. И площадь его равна 0.
(по вашему, если температура равна 0, то никакой температуры нет?)

Ilya83 в сообщении #1695534 писал(а):

то в результате весь лист бумаги (вся его площадь) будет покрыта отрезками

Нет, не будет. То есть так сделать можно, но для этого нужно несчетное число отрезков.
Говоря простыми словами -- "очень бесконечное". Вот, "складывая" такое число нулей, можно получить ненулевую площадь. Бесконечность -- она такая... парадоксальная!

[Ilya83]

wrest
Спасибо, гляну.

provincialka

Цитата:

по вашему, если температура равна 0, то никакой температуры нет?

Смотря на какой шкале смотреть.

Цитата:

Бесконечность -- она такая... парадоксальная!

Мы опять уперлись в парадокс.
Если я проведу ручкой линию и скажу, что все, я довел до 0. Потом возьму микроскоп x100 и увижу, что я таки не довел немного. Потом доведу линию под микроскопом x100, возьму микроскоп x1000 и увижу, что я таки не довел немного. Так можно продолжать до $\infty$.

И похоже мы уже уходим в Off Topic.

Всем большое спасибо за обсуждение!

[wrest]

Ilya83 в сообщении #1695549 писал(а):

Так можно продолжать до $\infty$.

И похоже мы уже уходим в Off Topic.

Да, это совсем не школьная тема. Тут начинается высшая математика.

[dgwuqtj]

Ilya83 в сообщении #1695549 писал(а):

Так можно продолжать до $\infty$.

Микроскопы кончатся довольно быстро.

[Лукомор]

Ilya83 в сообщении #1695534 писал(а):

Можно взять для примера тот самый египетский треугольник.

Можно, но Вам этот пример не понравится...

-- Вс июл 27, 2025 15:24:26 --

Ilya83 в сообщении #1695463 писал(а):

Если я возьму веревку, свяжу в узилок и растяну в высоту, я получу, допустим, h=10, B=1. Если затем я эту же петлю растяну в ширину, я получу h=1, B=10. Площадь фигуры при этом не изменится.

Если затем я возьму у Вас эту же петлю, и снова растяну в высоту, я получу, допустим, $h=9$ и $B=2$.
Площадь фигуры при этом изменится $S = hB = 9\cdot 2 = 18$
(Просто у меня пальцы толще! )

[Лукомор]

Ilya83 в сообщении #1695493 писал(а):

Если я возьму шарик и залью в него 1л воды. Потом я могу придать этому шарику форму куба или тетраэдра. Но там как был 1л воды так и остался.

Там шарик, при придании ему формы куба, растянется сильнее
(площадь поверхности увеличится), а при придании ему формы тетраэдра
растянется еще сильнее, и может даже лопнуть.
Применительно к исходной Вашей задаче, нужно взять резинку, связать ее концы, и сделать из нее прямоугольник, со сторонами $A$ и $B$.
Теперь будем наклонять сторону $A$, превращая прямоугольник в параллелограмм. При этом следим, чтобы высота параллелограмма оставалась равной высоте исходного прямоугольника $h$.
Тогда боковая сторона параллелограмма $A$ будет растягиваться с уменьшением угла между сторонами все сильнее, пока резинка не порвется.
И в этом случае, да!, площадь параллелограмма будет оставаться постоянной,
в полном соответствии с формулой $S=hB$.
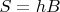
Если же боковая сторона параллелграмма $A$ не резиновая, а титановая имеет постоянную длину, то при ее повороте будет уменьшаться высота параллелограмма $h$, и вместе с нею площадь параллелограмма.