Фазовая развёртка по модулю — геометрический подход к анализу чисел
https://drive.google.com/file/d/1vh9fkAc7qzQPLUXsicxN_RxVOgsh_VIt/view?usp=drive_linkСуть метода
Фазовая развёртка отображает натуральные числа на двумерную решётку:
Фаза (x): n mod m (остаток от деления на модуль)
Уровень (y): целая часть от деления n/m
Геометрически это можно представить как намотку числовой прямой на цилиндр с шагом m. Числа 0, m, 2m и так далее выстраиваются по одной вертикали.
Ключевые свойства
Простые числа при m=6 лежат только в фазах 1 и 5, так как числа с фазами 0, 2, 3 и 4 делятся на 2 или 3.
Кратные числа образуют прямые линии. Например, кратные 2 при m=6 имеют последовательность фаз 2, 4, 0, 2 и так далее.
"Дырки" в решётке соответствуют простым числам — они занимают позиции, не занятые кратными паттернами.
Доказательство невозможности равенства

через фазовую развёртку
Теорема: Не существует натуральных чисел ( a, b, c geq 1 ), удовлетворяющих уравнению:

1. Векторное представление в фазовой развёртке
Выберем модуль развёртки

. Каждое число n представляется как вектор:

Для суммы

:
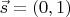
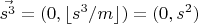
2. Разложение суммы кубов
Используем неполное биномиальное разложение:

В векторной форме:
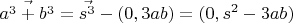
3. Условие равенства

Если равенство существует, то:

Из условия

следует:

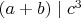
4. Анализ уровней
Сравним координаты:
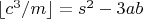
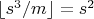
Разность уровней:

5. Конфликт в разложении
Представим

как:

где
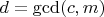
. Тогда:

Требуется одновременное выполнение:


Но для

:

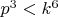

При этом:
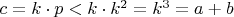
Но из
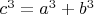
следует

, что приводит к противоречию при

.
6. Геометрическая интерпретация
В фазовой развёртке по

:
- Вектор
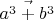
имеет ненулевую вертикальную компоненту

- Вектор

должен совпадать с
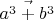
, но:

делающий равенство невозможным.
Вывод:
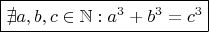
Это согласуется с доказательством Эйлера для случая

Великой теоремы Ферма. Паразитный член

в разложении всегда нарушает коллинеарность векторов. Фазовая развёртка по модулю — геометрический подход к анализу чисел.
Аналогично через неполное разложение Бинома Ньютона ВТФ
Не доказывается для любого n>2.
Причина: даже на векторной плоскости, любой вектор само пересекается в каждой точке то есть взяв n-1 векторов на длину n - мы получим пересечение не только в точке n, но также в любой точке вектора. Для такой конструкции не просто найти Инвариант. Как минимуму нам надо иметь конструкцию n-ой мерности. Поэтому все доказательства по определению невозможны пока не найден Инвариант для

.