Вот код, который фиксирует суффикс и префикс длины

искомого квадрата и использут функцию
sqrtintmod2(N,q) и параллелизацию для эффективного нахождения таких квадратов. Если ищем квадраты длины

, то

нужно оптимально брать равным примерно
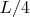
.
Код:
export(isNULL);
export(asqrtintmod2);
{ piramid_len(L) = my(rings, fd, ld, s);
rings = vector(10, i, (i-1)^2);
fd = rings \ 10; \\ first digits
ld = rings % 10; \\ last digits
s = max(1,L\4);
parforvec(v=vector(s,i,[if(i<s,1,5),#ld]),
my(suff, pref);
suff = fromdigits(apply(x->ld[x],v));
pref = fromdigits(Vecrev(apply(x->fd[x],v)));
foreach(asqrtintmod2(10^s,suff), r,
forstep(t=sqrtint(pref*10^(L-s)-1)+1, sqrtint((pref+1)*10^(L-s)-1), r,
my( d = digits(t^2) );
if(!issquare(d[(L+1)\2]),next);
for(i=s+1,(L-1)\2, if( !issquare(d[i]*10+d[L+1-i]), next(2) ); );
print([pref,suff]," ",r," ",t," ",t^2);
);
);
);
}
Результаты такие:
Код:
? piramid_len(3)
[1, 6] Mod(4, 10) 14 196
[8, 1] Mod(9, 10) 29 841
? piramid_len(5)
[38, 16] Mod(46, 50) 196 38416
? piramid_len(7)
[60, 44] Mod(12, 50) 2462 6061444
[83, 61] Mod(31, 50) 2881 8300161
? piramid_len(9)
[380, 16] Mod(496, 500) 19496 380094016
? piramid_len(11)
[668, 144] Mod(488, 500) 258488 66816046144
? piramid_len(13)
[3003, 6116] Mod(454, 2500) 1732954 3003129566116
? piramid_len(15)
[6314, 9664] Mod(608, 2500) 25128108 631421811659664
? piramid_len(17)
[41260, 94569] Mod(25587, 50000) 203125587 41260004094094569
? piramid_len(19)
? piramid_len(21)
? piramid_len(23)
? piramid_len(25)
[3003260, 4456196] Mod(1635486, 2500000) 1732991635486 3003260008664441094456196
? piramid_len(27)
[1208060, 401156] Mod(1237534, 2500000) 10991178737534 120806010040419494060401156
? piramid_len(29)
[3001800, 4116996] Mod(2018114, 2500000) 173257034518114 30018000010010946096194116996
[6620468, 1494544] Mod(5612, 625000) 257302705005612 66204682003204990560951494544
? piramid_len(31)
? ##
*** last result: cpu time 50min, 15,050 ms, real time 7min, 45,920 ms.
Как видим, поиск квадратов длины 31 потребовал около 8 минут. Так что, можно поискать и дальше, если есть желание.