Не могу понять определение кокасательного пространства Зарисского как факторпространства

. Здесь (если я правильно поняла) за

обозначается векторное пространство всех функциональных ростков, которые равны нулю в точке

а за

--- векторное подпространство тех функциональных ростков, которые имеют в точке

нуль второго порядка, т.е. каждый такой росток представляется функцией
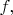
производная которой также равна нулю в точке

В частности, дифференциал функции

в точке

определяется как элемент

Очевидно, что функция

обращается в нуль в точке

т.е. представляет некоторый росток из

Далее не совсем понятно: "Его класс вычетов по модулю

и есть по определению,

"
Интуитивно понимаю, что "подбираемся" к линейной части приращения функции и в голову приходит ряд Тейлора функции

в точке

Помогите разобраться, пожалуйста.