ХРИН 07 Хронометрическое дифференцирование

[Утундрий]

В этом параграфе мы введём хронометрические дифференциальные операторы $\partial$ и $\nabla_i$ , выясним их смысл и рассмотрим их действие на хинвариантах и некоторых хитензорах.

Ниже будут использованы:

$1)$ Стандартное обозначение для коммутатора двух операторов

$$\left[ A,B \right] \equiv A \, B- B \, A .$$

$2)$ Сокращённое обозначение для циклической суммы

$$Q_{ikm}+\langle i k m \rangle \equiv Q_{ikm}+Q_{kmi}+Q_{mik} .$$

$3)$ Тот факт, что в приведенной выше краткой записи циклической суммы можно циклически же переставлять индексы в "циклируемом" выражении

$$Q_{ikm}+\langle i k m \rangle =Q_{kmi}+\langle i k m \rangle =Q_{mik}+\langle i k m \rangle .$$

§7 Хронометрическое дифференцирование

В предыдущем параграфе мы завершили изучение алгебры хитензоров и теперь переходим к анализу. Другими словами, мы хотим научиться дифференцировать "хорошие" величины так, чтобы получалось тоже что-то "хорошее". Как показано ниже, если просто взять от хинварианта частную производную по какой либо координате, то результат, вообще говоря, не будет ни хинвариантом ни хивектором. Можно, однако, составить такие линейные комбинации частных производных, которые переведут хинвариант снова в хинвариант или сделают из хинварианта хивектор. Приступим к построению таких комбинаций.

Для этого сперва освежим в памяти ряд формул из §2, относящихся к хронометрическим преобразованиям:

$$x_{,0}^{\widetilde 0}= \sigma \, \dfrac{h}{\widetilde h}\ne 0, \qquad x_{,i}^{\widetilde 0}=\dfrac{x_{,i}^{\widetilde s} \, a_{\widetilde s} - \sigma a_i}{\widetilde h},\qquad x_{,0}^{\widetilde i}=0.$$

Заметим также, что поскольку $0=\delta^i_0=x^{i}_{,\widetilde \alpha} \, x_{, 0}^{\widetilde \alpha}=x^{i}_{,\widetilde 0} \, x_{, 0}^{\widetilde 0}$ и $x_{, 0}^{\widetilde 0}\ne 0$, то

$$x^i_{, \widetilde 0}=0.$$

Рассмотрим произвольный хинвариант $\overline \rho$ и распишем его "временну́ю" частную производную с учётом приведенных выше равенств:
$\overline \rho_{,0}=\overline \rho_{,\widetilde \alpha} \, x^{\widetilde \alpha}_{,0}=\overline \rho_{,\widetilde 0} \, x^{\widetilde 0}_{,0}= \sigma \, \dfrac{h}{\widetilde h}\, \overline \rho_{,\widetilde 0} $
Замечаем и обозначаем хинвариантную комбинацию

$$\overline \rho_{.0} \equiv \dfrac 1 h \, \overline \rho_{,0} =\sigma \, \overline \rho_{.\widetilde 0} \eqno (7,1)$$

Повторяя выкладки для псевдо-хинварианта $\overset{*} \rho$, находим

$$\overset{*} \rho_{.0} =\operatorname{sign} \overset{\; \_} J \cdot \sigma \, \overset{*} \rho_{.\widetilde 0} \eqno (7,2)$$

Результат вполне ожидаемый, поскольку псевдо-хинвариант отличается от хинварианта лишь наличием в законе преобразования дополнительного постоянного множителя $\operatorname{sign} \overset{\; \_} J$, безразличного к любому дифференцированию. Поэтому все формулы данного параграфа сохраняют свой вид при взаимной замене хитензоров на псевдо-хитензоры того же типа.

Теперь посмотрим на $(7,1)$ как на операцию и применим её к произвольному хивектору $\overset{\;\_} E{}^{i}$:
$\overset{\;\_} E{}^{i}_{.0}=\sigma \, \overset{\;\_} E{}^{i}_{.\widetilde 0}=\sigma \, \dfrac {1}{\widetilde h} \left( x^{i}_{,\widetilde s} \, \overset{\;\_} E{}^{\widetilde s} \right){}_{,\widetilde 0}= \sigma \, x^{i}_{,\widetilde s} \, \dfrac {1}{\widetilde h} \, \overset{\;\_} E{}^{\widetilde s}_{,\widetilde 0}= \sigma \, x^{i}_{,\widetilde s} \, \overset{\;\_} E{}^{\widetilde s}_{.\widetilde 0}$
То есть, хивектор остался хивектором.

Тем же способом находим $\overset{\;\_} E_{i.0}=\sigma \, x_{,i}^{\widetilde s} \, \overset{\;\_} E_{\widetilde s .\widetilde 0}$

Далее, пользуясь правилом дифференцирования произведения

$$\left( A \, B \right){}_{.0}=A_{.0}B+A\,B_{.0}$$

и тем фактом, что любой хитензор можно представить в виде конечной суммы прямых произведений хивекторов (аналогично §6), заключаем, что для произвольного хитензора $\overset{\_} U{}^{i \ldots k}_{m \ldots n}$ справедливо

$$\overset{\_} U{}^{i \ldots k}_{m \ldots n . 0}=\sigma \, x^{i}_{, \widetilde p} \ldots x^{k}_{, \widetilde q} \, x_{, m}^{\widetilde r} \ldots x_{, n}^{\widetilde s} \, \overset{\_} U{}^{\widetilde p \ldots \widetilde q}_{\widetilde r \ldots \widetilde s . \widetilde 0} \eqno (7,3)$$

Итак, операция $(7,1)$ переводит произвольный хитензор в хитензор того же типа, но с противоположной $T$-чётностью.

Любопытно, что $(7,1)$ может сделать хинвариантной даже не хинвариантную величину. Например, по доказанному выше, $\left( \ln \overset{\,\_} g \right){}_{.0}={\overline g}^{ik}{\overline g}_{ik.0}$ — хинвариант, хотя $\ln \overset{\,\_} g$ хинвариантом не является.

Вернёмся к произвольному хинварианту $\overline \rho$ и распишем его "пространственные" частные производные:
$\overline \rho_{,i}=\overline \rho_{,\widetilde \alpha} \, x^{\widetilde \alpha}_{,i}=\overline \rho_{,\widetilde 0} \, x^{\widetilde 0}_{,i}+\overline \rho_{,\widetilde s} \, x^{\widetilde s}_{,i}=\overline \rho_{.\widetilde 0} \left( x_{,i}^{\widetilde s} \, a_{\widetilde s} - \sigma a_i \right)+\overline \rho_{,\widetilde s} \, x^{\widetilde s}_{,i}=$
$=x^{\widetilde s}_{,i} \left( \overline \rho_{,\widetilde s}+a_{\widetilde s} \, \overline \rho_{.\widetilde 0} \right)-a_i \, \overline \rho_{.0}$
Отсюда извлекаем следующий хивектор

$$\overline \rho_{.i} \equiv \overline \rho_{,i} + a_i \, \overline \rho_{.0} =x^{\widetilde s}_{, i} \, \overline \rho_{.\widetilde s} \eqno (7,4)$$

Выражения $(7,1)$ и $(7,4)$ назовём хронометрическими производными.

Чтобы раскрыть их смысл, внимательно посмотрим на дифференциал
$d \, \overline \rho = \overline \rho_{,0} \, dx^0+ \overline \rho_{,i} \, dx^i= \overline \rho_{.0} \, h \, dx^0+\left( \overline \rho_{.i} - a_i \, \overline \rho_{.0} \right) dx^i$
Вспоминая $(1,3)$ это выражение можно переписать так

$$d \, \overline \rho = \overline \rho_{.0} \, \delta \overline \tau+\overline \rho_{.i} \, dx^i \eqno (7,5)$$

Положим $dx^i=0$, тогда $\delta \overline \tau=\delta s$. То есть $ \overline \rho_{.0}$ является производной от $ \overline \rho$ по собственному времени тела отсчёта (которое, напомним, покоится относительно рассматриваемой системы отсчёта).

Уравнение $\delta \overline \tau=0$ задаёт в четырёхмерном пространстве событий локальную гиперплоскость одновременности к событию $x$. Поэтому величины $\overline \rho_{.i}$ представляют собой градиент $ \overline \rho$, вычисленный в направлении $dx^i$ так, что берётся разность значений $ \overline \rho$ в одновременных точках-событиях.

Мы уже знаем, что $\overline \rho_{.0i}$ и $\overline \rho_{.i0}$ — хивекторы. Найдём их разность.
$\overline \rho_{.0i}=\left(\overline \rho_{.0} \right){}_{,i}+a_i \, \overline \rho_{.00}=\left(\dfrac 1 h \overline \rho_{,0} \right){}_{,i}+a_i \, \overline \rho_{.00}=\dfrac 1 h \overline \rho_{,0i}+a_i \, \overline \rho_{.00}-\dfrac {h_{,i}}{h} \overline \rho_{.0}$
$\overline \rho_{.i0}=\dfrac 1 h \left(\overline \rho_{.i} \right){}_{,0}= \dfrac 1 h \, \left(\overline \rho_{,i} + a_i \, \overline \rho_{.0} \right){}_{,0}=\dfrac 1 h \overline \rho_{,i0}+a_i \, \overline \rho_{.00}+\dfrac {a_{i,0}}{h} \overline \rho_{.0}$
$\overline \rho_{.0i}-\overline \rho_{.i0}=-\dfrac 1 h \left(h_{,i}+a_{i,0}\right)\overline \rho_{.0}$
Что с учётом $(5,7)$ даёт

$$\overline \rho_{.0i}-\overline \rho_{.i0}=\overline f_i \, \overline \rho_{.0}\eqno (7,6)$$

Проделаем аналогичные выкладки для "пространственных" компонент

$\overline \rho_{.ik}-\langle ik \rangle=\left(\overline \rho_{.i} \right){}_{,k}+a_k \, \overline \rho_{.i0} -\langle ik \rangle=\left(\overline \rho_{,i} + a_i \, \overline \rho_{.0}\right){}_{,k}-a_i \, \overline \rho_{.k0} -\langle ik \rangle=$
$=a_{i,k} \, \overline \rho_{.0}+a_i \left(\overline \rho_{.0,k}-\overline \rho_{.k0} \right)-\langle ik \rangle=a_{i,k} \, \overline \rho_{.0}+a_i \left(\overline \rho_{.0k}-a_k \, \overline \rho_{.00} -\overline \rho_{.k0} \right)-\langle ik \rangle=$
$=\left(a_{i,k}+a_i \, \overline f_k-\langle ik \rangle \right) \overline \rho_{.0}$
Снова глядя на $(5,7)$, получаем

$$\overline \rho_{.ik}-\overline \rho_{.ki}=-2 \, \overline {\omega}_{ik} \, \overline \rho_{.0}\eqno (7,7)$$

До этого момента мы использовали только индексную запись хронометрических производных. Для большей наглядности введём также хронометрические дифференциальные операторы, действующие на функции слева

$$\partial \equiv \dfrac 1 h \, \dfrac {\partial}{\partial x^0}\; , \qquad \nabla_i \equiv \dfrac {\partial}{\partial x^i}+a_i \, \partial \eqno (7,8)$$

Эти операторы, рассматриваемые как множители, имеют следующие физические размерности

$$[[ \partial]]=\text{сек}^{-1} \, , \qquad [[\nabla_i]]=1 \eqno (7,9)$$

Теперь $(7,6)$ и $(7,7)$ можно переписать так

$$\left\{ {\begin{array}{rcl} \left[ \nabla_i , \partial \right]&=& \overline f_i \, \partial \\ \dfrac 1 2 \left[ \nabla_i , \nabla_k \right] &=& \overline {\omega}_{ik} \, \partial \\ \end{array} } \right. \eqno (7,10)$$

Мы видим, что ненулевые $\overline f_i$ и $\overline {\omega}_{ik}$ приводят к некоммутативности операторов $(7,8)$, кроме случая действия на не зависящие от $x^0$ функции.

Продолжим пополнение зоопарка "хороших" величин. Рассмотрим следующее антисимметричное выражение
$\overset{\;\_} E_{i,k}-\langle ik \rangle=\left( x^{\widetilde s}_{,i} \, \overset{\;\_} E_{\widetilde s} \right){}_{,k} -\langle ik \rangle=x^{\widetilde s}_{,i} \, \overset{\;\_} E_{\widetilde s, \widetilde 0}\, x^{\widetilde 0}_{,k}+x^{\widetilde s}_{,i} \, \overset{\;\_} E_{\widetilde s, \widetilde m}\, x^{\widetilde m}_{,k}-\langle ik \rangle=$
$=x^{\widetilde s}_{,i} \, \overset{\;\_} E_{\widetilde s. \widetilde 0}\, \left( x^{\widetilde m}_{,k}\, a_{\widetilde m}-\sigma \, a_k \right)+x^{\widetilde s}_{,i} \, \overset{\;\_} E_{\widetilde s, \widetilde m}\, x^{\widetilde m}_{,k}-\langle ik \rangle=x^{\widetilde s}_{,i} \, x^{\widetilde m}_{,k} \, \overset{\;\_} E_{\widetilde s. \widetilde m} -a_k \, \overset{\;\_} E_{i.0} -\langle ik \rangle$
Откуда следует
$\overset{\;\_} E_{i.k}-\langle ik \rangle=\overset{\;\_} E_{i,k}+a_k \, \overset{\;\_} E_{i.0} -\langle ik \rangle=x^{\widetilde s}_{,i} \, x^{\widetilde m}_{,k} \, \overset{\;\_} E_{\widetilde s. \widetilde m} -\langle ik \rangle$
Что можно переписать в виде

$$\overset{\;\_} E_{i.k}-\overset{\;\_} E_{k.i}=x^{\widetilde s}_{,i} \, x^{\widetilde m}_{,k} \left( \overset{\;\_} E_{\widetilde s . \widetilde m} - \overset{\;\_} E_{\widetilde m . \widetilde s} \right) \eqno (7,11)$$

И это в точности закон преобразования хитензора.

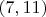
Выражение в левой части $(7,11)$ будем называть хитензор-ротор. Вычислим его значение для хивектора ускорения:
$\overline f_{i,k} -\langle ik \rangle=-\left[ \dfrac 1 h \left( h_{,i}+a_{i,0} \right) \right]{}_{,k}-\langle ik \rangle=- \dfrac 1 h \, a_{i,0k}+ \dfrac {1} {h^2} \, a_{i,0} h_{,k}-\langle ik \rangle$
$\overline f_{i.k} -\langle ik \rangle=\overline f_{i,k} +a_k \, \overline f_{i.0}-\langle ik \rangle=- \dfrac 1 h \, a_{i,0k}+ \dfrac {1} {h^2} \, a_{i,0} h_{,k}-a_i \, \overline f_{k.0}-\langle ik \rangle $
$2\, \overline \omega_{ik.0}=-\dfrac 1 h \left( a_{i,k}+a_i \, \overline f_k-\langle ik \rangle \right){}_{,0}=-\dfrac 1 h \, a_{i,k0}-\dfrac 1 h \, a_{i,0} \, \overline f_k-a_i \, \overline f_{k.0}-\langle ik \rangle$
$\overline f_{i.k} -\overline f_{k.i} -2\, \overline \omega_{ik.0}=\dfrac {1} {h^2} \, a_{i,0} \left( h_{,k}+h \, \overline f_k \right)-\langle ik \rangle=-\dfrac {1} {h^2} \, a_{i,0} \, a_{k,0} -\langle ik \rangle=0$

$$\overline \omega_{ik.0}=\dfrac 1 2 \left( \overline f_{i.k} -\overline f_{k.i} \right) \eqno (7,12)$$

Возникла (на первый взгляд неожиданная) связь между полями ускорения и вращения системы отсчёта. Однако неизбежность наличия связей между этими двумя хитензорами легко осознать, если вспомнить, что шесть компонент $\overline \omega_{ik}$ и $\overline f_i}$ составлены всего из четырёх величин: $h$ и $a_i$. Следовательно, уже по этой арифметической причине они не могут быть полностью независимы.

Приведём ещё одну связь подобного рода, опустив её несложный, но достаточно громоздкий вывод:

$$\overline \omega_{ik.m}+ \overline \omega_{ik}\, \overline f_m+\langle i k m \rangle=0 \eqno (7,13)$$

Отсюда следует, что циклическая сумма $\overline \omega_{ik.m}+\langle i k m \rangle$ является хитензором.

Докажем, что данное свойство справедливо для любого антисимметричного хитензора. Для этого снова воспользуемся основной идеей §6 и представим произвольный антисимметричный хитензор в виде $\overset{\,\_}{H}_{ik}=\sum \left( \overline p_i \overline q_k- \overline p_k \overline q_i \right)$, после чего циклическая сумма $\overset{\,\_}{H}_{ik.m}+\langle i k m \rangle$ примет вид
$\left( \overline p_i \overline q_k- \overline p_k \overline q_i \right){}_{.m}+\langle i k m \rangle=\overline p_{i.m} \overline q_k- \overline p_{k.m} \overline q_i+\overline p_i \overline q_{k.m}- \overline p_k \overline q_{i.m}+\langle i k m \rangle$
Теперь заменой $i \to m \to k \to i$ в первом и последнем слагаемом приведём её к очевидно хитензорной форме:

$$\left(\overline p_{m.k}-\overline p_{k.m}\right)\overline q_i+\overline p_i \left(\overline q_{k.m}-\overline q_{m.k}\right)+\langle i k m \rangle$$

Итак, для любого антисимметричного хитензора $\overset{\,\_}{H}_{ik}$ выражение $\overset{\,\_}{H}_{ik.m}+\overset{\,\_}{H}_{km.i}+\overset{\,\_}{H}_{mi.k}$ также является хитензором.

Сворачивая его с $\overset{*}e {}^{ikm}$ и приводя подобные, приходим к выводу, что выражение $\overset{*}e {}^{ikm}\, \overset{\,\_}{H}_{ik.m}$ является псевдо-хинвариантом.

Несколько преобразуем его при помощи соотношений из §4:
$\overset{*}e {}^{ikm}\, \overset{\,\_}{H}_{ik.m}=\dfrac {1}{\sqrt{\overset{\,\_} g}} \, \varepsilon^{ikm}\, \overset{\,\_}{H}_{ik.m}=\dfrac {1}{\sqrt{\overset{\,\_} g}}\left(\sqrt{\overset{\,\_} g}\, \overset{*}e {}^{ikm}\, \overset{\,\_}{H}_{ik}\right){}_{.m}=\dfrac {2}{\sqrt{\overset{\,\_} g}}\left(\sqrt{\overset{\,\_} g}\, \overset{\, *}{H}{}^m \right){}_{.m} $
Рассмотрим ещё хивектор
$\overset{*}e {}^{ikm}\, \overset{\, *}{H}_{k.m}=\dfrac {1}{\sqrt{\overset{\,\_} g}} \, \varepsilon^{ikm}\, \overset{\, *}{H}_{k.m}=\dfrac {1}{\sqrt{\overset{\, \_} g}}\left(\sqrt{\overset{\,\_} g}\, \overset{*}e {}^{ikm}\, \overset{\, *}{H}_k\right){}_{.m}=\dfrac {1}{\sqrt{\overset{\,\_} g}}\left(\sqrt{\overset{\,\_} g}\, \overset{\, \_}{H}{}^{mi} \right){}_{.m} $
В завершение перепишем $(7,12)$ и $(7,13)$ с использованием только "одноиндексных" величин:

$$\left\{ {\begin{array}{rcl} \dfrac {1}{\sqrt{\overset{\,\_} g}} \left(\sqrt{\overset{\,\_} g} \, \overset{*}\omega{}^i\right){}_{.0}&=&-\dfrac 1 2 \, \overset{*}e {}^{ikm}\, \overline f_{m.k} \\ \dfrac {1}{\sqrt{\overset{\,\_} g}} \left(\sqrt{\overset{\,\_} g} \, \overset{*}\omega{}^s \right){}_{.s} &=& -\overset{*}\omega{}^s \, \overline f_s \\ \end{array} } \right. \eqno (7,14)$$

Как видим, уже из хивекторов не так-то просто соорудить нечто хитензорное, размахивая наугад хронометрическими производными. Позже мы ведём т.н. "хинвариантные производные", являющиеся аналогом ковариантных производных четырёхмерной геометрии, которые позволят дифференцировать любой хитензор хинвариантным образом. Ну а пока что рассмотренных здесь объектов и доказанных фактов вполне достаточно для перехода к следующим параграфам, где будут рассмотрены уравнения электромагнитного поля.

Задача

Как изменяется $\dfrac {1}{\sqrt{\overset{\,\_} g}} \left(\sqrt{\overset{\,\_} g} \, \overset{\_}g{}^{is} \right){}_{.s}$ при хронометрических преобразованиях?

[Утундрий]

Ускорю процесс решения задачи.

Обозначим $\Upsilon^i \equiv \dfrac {1}{\sqrt{\overset{\,\_} g}} \left(\sqrt{\overset{\,\_} g} \, \overset{\_}g{}^{is} \right){}_{.s}$

Разложим $\overset{\_}g{}^{is}=\sum \overline u^i \overline u^s$, а $\sqrt{\overset{\,\_} g}$ оставим как есть.

Составим величину $\Xi^{\widetilde i} \equiv \Upsilon^{\widetilde i}-x^{\widetilde i}_{,k} \, \Upsilon^k$

Запишем $\Upsilon^i$ в следующем виде:

$$\Upsilon^i = \sum \overline u^{i} \dfrac {1}{\sqrt{\overset{\,\_} g}} \left(\sqrt{\overset{\,\_} g} \, \overline u^{s} \right){}_{.s}+\sum \overline u^{s} \, \overline u^{i}_{.s} $$

Заметим, что первое слагаемое — хивектор. Следовательно, оно выпадает из $\Xi^{\widetilde i}$ для которой, после небольшого преобразования, получается следующее выражение:

$$\Xi^{\widetilde i}=\sum \left( x^{\widetilde k}_{,s} \, \overline u^{\widetilde i}{}_{. \widetilde k}-x^{\widetilde i}_{,k} \, \overline u^{k}_{.s}\right) \overline u^{s}$$

Осталось найти разность в круглых скобках.

[Cos(x-pi/2)]

Мудрить таким неочевидным образом я не пробовал (и никогда не догадался бы), а просто преобразовывал данное в задаче выражение; хорошего ничего не получил:

(Оффтоп)

У меня вышла вот такая формула (как если бы выполнялось $(AB)_{.p}=A_{.p}B+A(B)_{.p}):$

$$\frac {1}{\sqrt{\overset{\,\_} g}} \left(\sqrt{\overset{\,\_} g} \, \overset{\_}g{}^{is} \right){}_{.s}\,=\,\frac{1}{2}\,\overset{\_}g{}^{kn}\,\overset{\_}g{}_{kn.s}\,\overset{\_}g{}^{is}\,+\,\overset{\_}g{}^{is}{}_{.s}$$

Хивекторного закона преобразования для неё у меня не вышло, вылезли вторые производные координат. Т.е., например, для $\overset{\_}g{}^{is}{}_{.p}$ получилось:

$$\overset{\_}g{}^{is}{}_{.p}\,=\,x^{\widetilde m}_{,p} \,x^i_{,\widetilde k} \,x^s_{,\widetilde n}\, \overset{\_}g{}^{\widetilde k \widetilde n}{}_{.\widetilde m} \,+\, (x^i_{,\widetilde k} \,x^s_{,\widetilde n})_{,\widetilde m}\,x^{\widetilde m}_{,p} \,\overset{\_}g{}^{\widetilde k \widetilde n}$$

Свёртки не устранили вторых производных. (Может быть ошибаюсь, и всё это неверно; не знаю.)

[Утундрий]

Ну, задача ценна не сама по себе, а только лишь в целя́х закрепления фокусов-покусов, использованных в параграфе. Впрочем, в одном месте далее она всё-таки сыграет (если не передумаю).

(СПОЙЛЕР)

Cos(x-pi/2) в сообщении #1680361 писал(а):

Хивекторного закона преобразования для неё у меня не вышло

И не должно было.

P. S. Только сейчас сообразил, что "диадикам" не обязательно складываться именно в метрику. Так что намеченный выше ход решения по сути даёт закон преобразования величины

$$\dfrac {1}{\sqrt{\overset{\,\_} g}} \left({\sqrt{\overset{\,\_} g}} \, \overline \sigma{}^{is} \right){}_{.s}$$

где $\overline \sigma{}^{is}$ — произвольный симметричный хитензор второго ранга.

[Утундрий]

На всякий случай напоминаю, что мы остановились на вычислении величины

$$U^{\widetilde i}_s \equiv x^{\widetilde n}_{,s} \, \overline u^{\, \widetilde i}_{. \widetilde n}-x^{\widetilde i}_{,n} \, \overline u^{\, n}_{.s}$$

которая при помощи несложных махинаций сводится к простому выражению...

[Cos(x-pi/2)]

(Оффтоп)

У меня выходит ноль; но, думаю, это неверно, раз $\Upsilon^i$ не хивектор. Пожалуй, дальше я пас.

[Утундрий]

Для начала просто распишем хинвариантные производные $U^{\widetilde i}_s \equiv x^{\widetilde n}_{,s} \, \overline u^{\, \widetilde i}_{. \widetilde n}-x^{\widetilde i}_{,n} \, \overline u^{\, n}_{.s}= x^{\widetilde n}_{,s} \left(\overline u{}^{\, \widetilde i}_{, \widetilde n}+a_{\widetilde n} \, \overline u{}^{\, \widetilde i}_{. \widetilde 0}\right)-x^{\widetilde i}_{,n}\left(\overline u^{\, n}_{,s}+a_s \, \overline u^{\, n}_{.0}\right)$
Теперь заметим, что $x^{\, \widetilde i}_{,n}\, \overline u^{\, n}_{.0}=\sigma \, \overline u^{\, \widetilde i}_{. \widetilde 0}$
После чего получим
$U^{\widetilde i}_s=x^{\widetilde n}_{,s} \, \overline u^{\, \widetilde i}_{, \widetilde n}-x^{\widetilde i}_{,n} \, \overline u^{\, n}_{,s}+\left(x^{\widetilde n}_{,s}\, a_{\widetilde n}-\sigma \, a_s \right)\overline u{}^{\, \widetilde i}_{. \widetilde 0} $
Ещё раз заметим, что последний член равен $x^{\widetilde 0}_{,s} \, \overline u{}^{\, \widetilde i}_{, \widetilde 0}$ и вместе с первым даёт $x^{\widetilde \alpha}_{,s} \, \overline u{}^{\, \widetilde i}_{, \widetilde \alpha}=\overline u{}^{\, \widetilde i}_{, s}$
Поэтому
$U^{\widetilde i}_s=\overline u{}^{\, \widetilde i}_{, s}-x^{\widetilde i}_{,n} \, \overline u^{\, n}_{,s}=\left(x^{\widetilde i}_{,n} \, \overline u^{\, n} \right){}_{, s}-x^{\widetilde i}_{,n} \, \overline u^{\, n}_{,s}=x^{\widetilde i}_{,ns} \, \overline u^{\, n} $

Осталось собрать всё в ответ.