Паразитные параметры катушки индуктивности

[Alex-Yu]

peregoudov в сообщении #1669039 писал(а):

Ну вот и до ссылки на авторитет в качестве аргумента докатились... ...А последняя фраза... тут они просто ошибаются. Нет таких статистических систем, в которых при квазистационарном изменении внешних параметров оставался бы гистерезис.

Нихрена себе заявленнице... Ну о чем после этого говорить...

И еще на счет авторитетов. Вопрос что как называть или не называть никакого объективно-физического смысла не имеет и иметь не может. Тут только общепринято или не общепринято. А что общепринято, это как раз к авторитетам. В любом случае называть банальную временную дисперсию гистерезисом -- идея более чем странная. Не говоря уж о ее полной необщепринятости.

P.S. Кстати, о релаксации. В феро- и ферримагнетиках на больших временах релаксация как раз приводит не к исчезновению, а к усилению гистерезиса. Все очень просто: за счет диффузии дефектов возникают потенциальные ямы для доменных стенок как раз в тех местах, где эти доменные стенки находятся. И сдвинуть эти доменные стенки с "насиженных" мест становится с течением времени все труднее и труднее. Это явление называется магнитной аккомодацией.

[EUgeneUS]

peregoudov в сообщении #1669039 писал(а):

Одного раза мало, чтобы дошло, нужно семь раз повторить, что погонная емкость подбиралась для правильного значения собственного резонанса катушки?

peregoudov в сообщении #1668754 писал(а):

Во-первых, пришлось в пять раз увеличить погонную емкость, чтобы получить правильный первый резонанс.

В пять раз, Карл, в пять!
Это никак не объясняется ни лаком на проводе, ни влиянием каркаса. А значит модель неверна.

peregoudov в сообщении #1669039 писал(а):

Я могу понять, когда у одного калькулятор сломался, но чтоб у всех разом... Добротность контура при расчете по сопротивлению на постоянном токе 11.5, с учетом дополнительного паразитного сопротивления в 15 Ом --- 10.

Вывод тут напрашивается очевидный: калькулятор или что-то другое сломалось на Вашей стороне.

1. Добротность катушки по определению: $Q_L = \frac{\omega L}{R}$
Для $R=11.2$ Ом, $L=7.4$ мГн, $f = 27$ кГц - $Q_L=112$
Для $R=11.2+15=26.2$ Ом, $L=7.4$ мГн, $f = 27$ кГц - $Q_L=48$
(выше для простоты я полагал $R=12$, получалось чуть меньше)
А вот как Вы получили $Q=1700$ - одному Богу известно.

2. Добротность Вашего контура, с учетом добавленного сопротивления 100 Ом, действительно очень близка к $10$.

-- 08.01.2025, 12:12 --

peregoudov в сообщении #1669039 писал(а):

Ну да, если конденсатор в схеме замещения соединяет первый виток одного слоя с последним витком следующего --- из этого же никак не следует, что напряжение на нем больше, чем на конденсаторе между двумя соседними витками

1. Для квазистатичного случая (область низких частот) распределение напряжения вдоль провода можно считать линейным.
2. А значит напряжение в "конденсаторе", который соединяет первый виток одного слоя с последним витком следующего будет в $2n$ больше, чем между витками. Где $n$ - количество витков в слое.
Для Вашей катушки раз в 30-50.
Этот факт, кстати, известен всем, кто мотал силовые трансформаторы.
3. В модели "межвитковой емкости" это означает, что энергия в этом конденсаторе в $(2n)^2$ раз больше чем в отдельном конденсаторе между соседними витками одного слоя. Или в $4n$ раз больше, чем в "межвитковых конденсаторах" во всем слое.
4. Если Вы этим пренебрегаете, то Ваша модель неверна уже для квазистатического случая.

-- 08.01.2025, 12:12 --

peregoudov в сообщении #1669039 писал(а):

По-моему, вам пора уже заканчивать этот балаган.

И действительно.

[EUgeneUS]

peregoudov в сообщении #1669039 писал(а):

При замыкании должно было бы меняться сопротивление на постоянном токе, а оно совпадает с расчетным.

peregoudov в сообщении #1668754 писал(а):

600 витков,

То есть сопротивление изменится на $1/600$.
"По сравнению с расчетным". Ага

-- 08.01.2025, 15:21 --

realeugene в сообщении #1668973 писал(а):

Нюанс в квадратичной зависимосии эффекта близости от числа слоёв. В отличие от скин-эффекта, который роли тут не играет.

Эффект близости - это и есть скин-эффект. Только геометрическая конфигурация проводника более сложная, чем бесконечный цилиндрический проводник.

[realeugene]

EUgeneUS в сообщении #1669088 писал(а):

Эффект близости - это и есть скин-эффект.

Теории разные. А в целом конечно всё электродинамика Максвелла.

[EUgeneUS]

realeugene в сообщении #1669089 писал(а):

Теории разные.

Заглянем в Библию (ЛЛVIII)

Цитата:

Рассмотрим распределение плотности тока по сечению проводника, в котором течет отличный от нуля полный переменный ток. На основании полученных в предыдущем параграфе результатов мы заранее можем ожидать, что при увеличении частоты ток будет в основном концентрироваться вблизи поверхности проводника. Это явление называют скин-эффектом (1)).

(1) В более общем смысле о скин-эффекте говорят во всех ситуациях, когда переменное электромагнитное поле (а с ним и вызываемые им токи) проникает лишь на относительно небольшую глубину в проводник.

Не будем спорить о определениях с Ландау и Лифшицем. Или будем?

-- 08.01.2025, 15:44 --
del

[Alex-Yu]

EUgeneUS в сообщении #1669090 писал(а):

Не будем спорить о определениях с Ландау и Лифшицем.

Эффект близости может быть и тогда, когда поле проникает на большую глубину. Если уж искать аналогии, то эффект близости это что-то вроде токов Фуко. Токи Фуко в проводе, вызванные магнитным полем порожденным токами в соседних проводах. Естественно, эти токи Фуко накладываются на "собственный" ток провода, который может быть распределен по проводу даже вообще однородно, или почти однородно. В результате суммарный ток может даже идти в сторону, противоположному "собственному" току. Хотя, конечно, не везде, только в некоторых частях сечения провода. Скин-эффект все же сильно от этого отличается.

[realeugene]

EUgeneUS в сообщении #1669090 писал(а):

Не будем спорить о определениях с Ландау и Лифшицем. Или будем?

Во-первых, откуда сделан вывод, что поле при эффекте близости проникает на ограниченную глубину? Вы уже ознакомились с теорией Баттерворта?

Во-вторых, ЛЛ2 в подобной терминологии всё-таки не авторитет. В справочнике 43 года разделяют скин-эффект и эффект близости. Скорее всего потому что так было принято разделять.

[Ignatovich]

peregoudov в сообщении #1668754 писал(а):

Я тут взялся переделывать лабораторную установку "Изучение резонанса в последовательном колебательном контуре" и столкнулся с неожиданными трудностями.

В лабораторной работе по свободным колебаниям в RLC контуре будут подобные проблемы при сопоставлении экспериментального и расчетного коэффициентов затухания. Об этом пишут в статье, ссылку на которую приводил ранее:
Similar problems arise in the experiment with damped oscillations in an RLC circuit. The resistance of the coil calculated from the oscillation damping is significantly higher
than the DC resistance measured by an ohmmeter. It is necessary to note that multilayer coils on plastic cores are used in both cases.

[Amw]

Ignatovich в сообщении #1669096 писал(а):

Об этом пишут в статье, ссылку на которую приводил ранее:
Similar problems...

А не пойти ли Вам на... какой-нибудь англоязычный форум

[realeugene]

Кто хотел первоисточников?

https://archive.org/details/experimenta ... 3/mode/1up
https://archive.org/details/experimenta ... 7/mode/1up
https://archive.org/details/experimenta ... 7/mode/1up
https://archive.org/details/experimenta ... 3/mode/1up

Amw в сообщении #1669106 писал(а):

А не пойти ли Вам на... какой-нибудь англоязычный форум

Учите лучше английский: пригодится.
По правилам этот форум двуязычный русско-английский. И давно уже не российский.

[EUgeneUS]

Alex-Yu в сообщении #1669092 писал(а):

Если уж искать аналогии, то эффект близости это что-то вроде токов Фуко.

Да, согласен. Эффект близости - это токи Фуко, а токи Фуко рассматриваются отдельно от скин-эффекта.
"Был неправ, вспылил".

[Ende]

Amw в сообщении #1669106 писал(а):

А не пойти ли Вам на... какой-нибудь англоязычный форум

Английский язык - второй официальный язык форума. И не надо таких выражений.

[EUgeneUS]

realeugene в сообщении #1669107 писал(а):

Кто хотел первоисточников?
https://archive.org/details/experimenta ... 3/mode/1up https://archive.org/details/experimenta ... 7/mode/1up https://archive.org/details/experimenta ... 7/mode/1up https://archive.org/details/experimenta ... 3/mode/1up

Спасибо, увлекательное чтение.

Только со ссылкой на вторую часть у Вас ошибка (ссылка на другую статью Баттерворта)
Вот правильная ссылка на вторую часть:
https://archive.org/details/experimenta ... 9/mode/1up

[peregoudov]

realeugene в сообщении #1669043 писал(а):

Десятилетиями инженеры пользовались подобными справочниками

Но я-то не инженер Меня не устраивает подход "возьмем формулу". Я хочу понять, откуда что берется.

realeugene в сообщении #1669043 писал(а):

Только великим спецам современности теперь нужно обязательно компьютерную модель.

Вы что-то путаете. Чтобы разобраться в существе вопроса, нужна не "компьютерная модель", а простая, желательно точно решаемая физическая модель, на которой эффект можно "пощупать руками".

Alex-Yu в сообщении #1669063 писал(а):

Вопрос что как называть или не называть никакого объективно-физического смысла не имеет и иметь не может. Тут только общепринято или не общепринято. А что общепринято, это как раз к авторитетам.

То есть вы сейчас как будто расписались, что с гистерезисом затеяли чисто филологический спор?

Alex-Yu в сообщении #1669063 писал(а):

Это явление называется магнитной аккомодацией.

И оно отменяет нулевое начало термодинамики? Ну, про равновесное состояние, к которому система в неизменных внешних условиях стремится.

EUgeneUS в сообщении #1669069 писал(а):

А значит модель неверна.

А почему она должна быть верной? Если модель Ландау --- это два бесконечных параллельных провода, одни во всей Вселенной? В катушке-то много чего еще вокруг накручено Модель Ландау --- это просто для ориентировки по порядку величины.

EUgeneUS в сообщении #1669069 писал(а):

1. Добротность катушки по определению: $Q_L = \frac{\omega L}{R}$
Для $R=11.2$ Ом, $L=7.4$ мГн, $f = 27$ кГц - $Q_L=112$
Для $R=11.2+15=26.2$ Ом, $L=7.4$ мГн, $f = 27$ кГц - $Q_L=48$
(выше для простоты я полагал $R=12$, получалось чуть меньше)
А вот как Вы получили $Q=1700$ - одному Богу известно.

А, ну, понятно Как говорил в таких случаях небезызвестный Munin, проблема в прокладке между креслом и клавиатурой.

EUgeneUS в сообщении #1669069 писал(а):

4. Если Вы этим пренебрегаете,

Во-во, нарисовать на схеме замещения конденсатор, подключенный к первому витку одного слоя и последнему витку следующего, а затем "пренебречь" этим подключением

EUgeneUS в сообщении #1669088 писал(а):

То есть сопротивление изменится на $1/600$.

Это если соседние витки в одном слое. Но тогда, наверное, и на всем другом мало скажется? А если первый виток одного слоя с последним соседнего? Там без малого 50 витков выходит.

EUgeneUS в сообщении #1669069 писал(а):

И действительно.

А зачем продолжаете?

Ignatovich в сообщении #1669096 писал(а):

В лабораторной работе по свободным колебаниям в RLC контуре будут подобные проблемы при сопоставлении экспериментального и расчетного коэффициентов затухания.

Это лабораторная работа у меня следующая на очереди

-- Пт янв 10, 2025 20:35:06 --

Напишу про скин-эффект в уединенном прямом круглом проводе.

Есть прямой бесконечный цилиндрический провод, по которому течет переменный ток частоты $\omega$. Ток в проводе удовлетворяет уравнению

$$ \Delta{\bf j}=-i\omega\mu_0\sigma{\bf j}, $$

$\sigma$ --- проводимость. По симметрии ток имеет только компоненту вдоль оси провода, а зависит она только от радиальной переменной, расписывая лапласиан в цилиндрических координатах, находим

$$ \frac1r\frac\partial{\partial r}r\frac{\partial j_z}{\partial r}=-i\omega\mu_0\sigma j_z. $$

Будем измерять расстояния в единицах радиуса провода, тогда возникает безразмерный параметр $d=R\sqrt{\mu_0\sigma\omega/2}$ --- отношение радиуса провода к глубине проникновения. Решением этого уравнения, конечным при $r=0$ и дающим единичный полный ток через сечение, является

$$ j_z(r)=\frac{aI_0(ar)}{2\pi I_1(a)},\quad a=(1-I)d. $$

Соответственно, множитель к сопротивлению за счет скин-эффекта --- просто мощность этого тока, нормированная на единицу при $d=0$

$$ f(d)=\int_0^1|j_z(r)|^2\,2\pi^2r\,dr. $$

Интеграл в принципе выражается через бессели, но проще привести график (красным) и асимптотики (зеленым и синим) при $d\ll1$ и $d\gg1$

$$ f(d)=1+\frac1{48}d^4+\ldots,\quad f(d)=\frac d2+\frac14+\ldots $$

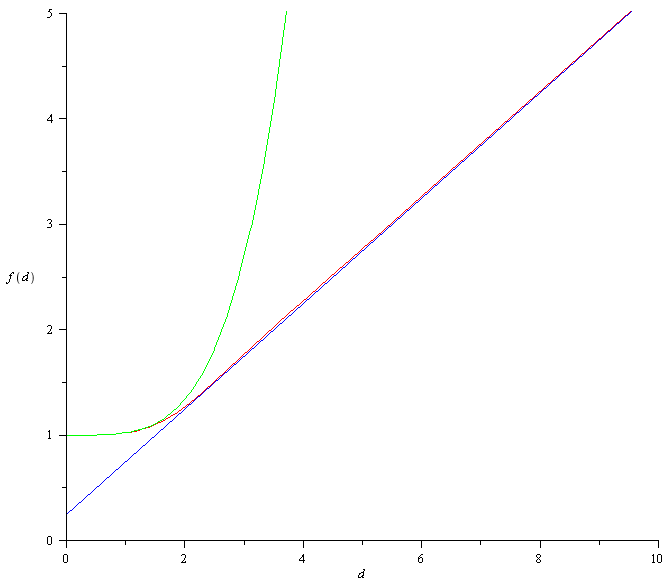
Как указано в стартовом сообщении, глубина проникновения 0.4 мм, а радиус провода 0.15 мм, то есть d=0.375 и поправка к сопротивлению составляет $4\cdot10^{-4}$ (четыре сотых процента).

-- Пт янв 10, 2025 20:41:41 --

Перепроверял тут статью, ссылку на которую дал Ignatovich. Интересное кино получается.

Рассмотрим модель бесконечно длинного многослойного соленоида, намотанного проводом квадратного сечения, так что намотка фактически представляет собой нарезанную на колечки толстостенную (намного толще глубины скин-слоя) трубу (рисунок слева).

http://sto68.narod.ru/figs/tape_solenoid.png

По симметрии магнитное поле в этой задаче имеет только $B_z$ компоненту, а ток --- только $j_\phi$ компоненту, причем обе величины зависят только от $r$. Если бы труба не была нашинкована на колечки, то за счет скин-эффекта ток собрался бы в самом внутреннем слое. Нарезка гарантирует, что в каждом квадратике полный ток один и тот же. Поскольку от $z$ ничего не зависит, нарезку по  $z$ можно убрать, оставив только нарезку по слоям (картинка справа).

Магнитное поле в каждом слое удовлетворяет уравнению

$$ \frac1r\frac\partial{\partial r}r\frac{\partial B_z}{\partial r}=-i\omega\mu_0\sigma B_z. $$

Его общее решение

$$ B_z(r)=\alpha I_0(ar)+\beta K_0(ar),\quad a=(1-I)d,\quad d=h\sqrt{\mu_0\sigma\omega/2}, $$

$h$ --- толщина слоя (расстояния измеряем в толщинах слоя).

Из теоремы о циркуляции следует, что магнитное поле в каждом слое прирастает на одну и ту же величину, без ограничения общности на 1, поэтому постоянные $\alpha$ и $\beta$ могут быть определены из граничных условий

$$ B_z(c-n)=n,\quad B_z(c-(n+1))=n+1,\quad n=0,\ldots, N-1, $$

$c$ --- внешний диаметр трубы, нумерация слоев идет извне вовнутрь. Поле вне трубы равно нулю.

Ток определяется из уравнения $\nabla\times{\bf B}=\mu_0{\bf j}$ и равен

$$ \mu_0j_\phi(r)=-\frac{d B_z(r)}{dr}. $$

Ниже привожу графики зависимости поля и тока (красная кривая --- вещественная часть, зеленая кривая --- мнимая часть, синяя кривая --- модуль) от радиальной координаты для случая $c=40$, $N=20$ и двух значений $d=0.1$ и $d=0.5$.

http://sto68.narod.ru/figs/Bz0_1.gif

http://sto68.narod.ru/figs/jphi0_1.gif

http://sto68.narod.ru/figs/Bz0_5.gif

http://sto68.narod.ru/figs/jphi0_5.gif

Видно, что во внутренних слоях нарастает неоднородность распределения тока. Чтобы распределение тока было примерно однородным (мелкая зубчатость все равно сохранится, даже в пределе $d\to0$), нужно, чтобы толщина скин-слоя была порядка полной толщины стенки трубы, того, что она порядка толщины слоя, недостаточно.

Непонятно также название "эффект близости". При раздвижке слоев он никуда не пропадает, что видно из рисунков ниже.

http://sto68.narod.ru/figs/Bz0_5a5.gif

http://sto68.narod.ru/figs/jphi0_5a5.gif

То есть это скорее эффект, связанный с увеличением индукции поля по мере перехода к внутренним слоям.

[EUgeneUS]

peregoudov в сообщении #1669419 писал(а):

Это если соседние витки в одном слое. Но тогда, наверное, и на всем другом мало скажется?

Скажется. Даже один короткозамкнутый виток убьёт добротность чуть менее, чем полностью.