Законы сохранения при абсолютно упругом ударе на плоскости

[pppppppo_98]

StudentV в сообщении #1660633 писал(а):

Но ведь в результате опыта величина $X$ примет какое-то значение, несмотря на нулевую вероятность того, что она примет именно это значение.

результат любого опыта в физике записывается в математических терминах $x\in[x_0-\varepsilon, x_0+\varepsilon]$, где $\varepsilon$ - погрешность, зависящая от точности оборудования, методики постановки эксперимента, систематических ошибок и прочяя...Здесь неявно предполагается гаусово распределение. 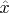Или еще более обобщенно проведя много экспериментов - а физика наука об повторяемых результата и предполагая независимость измерений (система измерения без памяти и не зависит от предыдущих результатов) вы получите распределение семпл $(x_0,x_1\dots x_in)$ из распределения плотность вероятности случайной величины $P(x| \hat{x})$, где $\hat{x}$ - истинное значение измеряемой случайной величины X, а x - показания прибора. 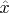В случае действительных величин нужно заменить x на $x\in[x_1, x_2]$, $\hat{x}$на $\hat{x}\in[\hat{x}_1, \hat{x}_2]$. По сепмлу предполагая функциональную форму закона распределения вы оцениваете параметры и восстанавливаете распределение $P(x| \hat{x})$

-- Пн ноя 11, 2024 15:45:24 --

drzewo в сообщении #1661179 писал(а):

Мой оппонент просто начитался Венцель.

Да это не важно ... Венцель - по жизни военным статистиком была, хлеб зря не жевала

[miflin]

(Оффтоп)

drzewo в сообщении #1661179 писал(а):

Венцель

pppppppo_98 в сообщении #1661183 писал(а):

Венцель

Это кто?