Я создал довольно много тем в междисциплинарном разделе, эту тоже мог создать там, но мне кажется в него заходит довольно мало народу, поэтому прошу знатоков иногда его посещать.
Я занимаюсь научной работой, конкретно квантовой химией, и мне хочется закодить какие-то собственные алгоритмы расчётов. Сейчас перспективной для меня темой выглядит реализация BOMD расчётов для предсказания масс-спектров молекул:
topic158174.htmlЭто достаточно понятная задача, которая может принести мне какие-то деньги. Здесь я хочу спросить вот о чём: если я реализую этот самый BOMD, насколько будет перспективно, и насколько сложно, попробовать хотя бы частично научиться заменить ньютоновскую механику квантовой, или придумать какие-то костыли, приближения. Я слышал что в молекулярной динамике (моделирование жидких сред) такие костыли используются.
Если непонятно, вот конкретный пример. Возьмём перегруппировку Маклафферти для молекулы 2-пентанона (точнее её иона):
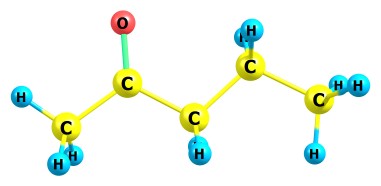
->
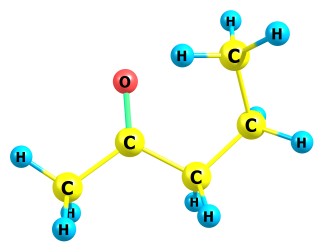
->
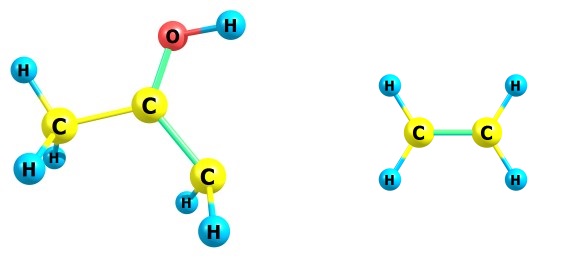
Можно в моделировании "расшатать" случайным образом эту молекулу, просчитать BOMD-траекторию её ядер; с некоторой вероятностью получится структура на последнем рисунке, и эта вероятность даст интенсивность иона C3OH6 в масс-спектре. Можно ли улучшить предсказание этой интенсивности, придумав через знание квантовой механики какой-то костыль, приближенный подход к предсказанию траектории ядерного уравнения Шредингера этой молекулы?