Знакомство с обучением нейронной сети

[sergey zhukov]

Сегодня решил попробовать научить нейронную сеть аппроксимировать функцию одной переменной. Просто чтоб почувствовать, как это делается. Раньше я обучением нейронных сетей не занимался.

Нарисовал сеть из двух слоев по пять нейронов с сигмоидой, и у каждого по пять входов. Плюс один выходной нейрон сети. Получилось 55 весов в сети. Обучал я ее так. Для каждого примера по очереди "дергал" все 55 весов, после чего для каждого примера корректировал веса по найденному градиенту (если ошибка ответа на данный пример при подвижке данного веса на фиксированный $\delta x$ уменьшается на $\Delta$, то я двигал этот вес на $\alpha\Delta$). Так по очереди перебирал все примеры многократно по порядку. И получилось как-то странно: хотя на каждом примере после корректировки весов ошибка для этого примера всегда уменьшается, но процесс даже близко не сходится к нулевой ошибке для каждого примера (хотя это точно возможно). Выглядит так, как-будто пока сеть учит остальные примеры, ее ошибка на данном примере восстанавливается до исходного состояния, и веса на каждом цикле обучения на наборе просто ходят по кругу. Что-то не так я тут сделал?

[mihaild]

А какая функция - точно ли она сколь-нибудь хорошо приближается такой архитектурой?
Попробуйте посмотреть, какие получаются значения весов и градиентов - может быть что-то взрывается или наоборот умирает.
Как процесс зависит от $\alpha$?

Обучение по одному примеру будет работать только при довольно малом шаге. Стандартный способ - минибатчи, считать градиенты по нескольким примерам сразу, и сдвигать на сумму.

[gevaraweb]

Почему у вас 55 весов? По рассказу у меня так не получается.
Сигмоида для регрессии не используется, лучше Релу, если аргумент и функция неотрицательные, либо без нее.
Вообще регрессию таким количеством нейронов не решить, нужно либо тысячи нейронов, либо тысячи эпох.
Для ручного счета возьмите пример, где мало данных, 1-2.

[Mihaylo]

gevaraweb в сообщении #1657123 писал(а):

Почему у вас 55 весов? По рассказу у меня так не получается.

Видимо так:
Первый слой - 5 нейронов по 5 синапсов
Второй слой - 5 нейронов по 5 синапсов
Выходной - нейрон с 5 синапсами.
Синапсов смещения нет.
Только я не понял, у нейросети 5 входов?

-- 03.10.2024, 19:31 --

sergey zhukov в сообщении #1657111 писал(а):

Обучал я ее так. Для каждого примера по очереди "дергал" все 55 весов, после чего для каждого примера корректировал веса по найденному градиенту (если ошибка ответа на данный пример при подвижке данного веса на фиксированный $\delta x$ уменьшается на $\Delta$, то я двигал этот вес на $\alpha\Delta$). Так по очереди перебирал все примеры многократно по порядку.

Тут я бы уточнил, ведь градиенты весов надо до последнего копить в отдельном массиве и "дёргать веса" можно хотя бы когда пример полностью прошел вперед (forward) и потом назад (backward). Это минимум (называется SGD). Обычно веса не трогают пробежавшись по ~20-500 примерам (это называют пакетом примеров или мини-батчем, а сам алгоритм Mini-batch GD, его еще дооснащают каким-нибудь алгоритмом инерции и так он становится Adam, например).

[gevaraweb]

Mihaylo в сообщении #1657230 писал(а):

Видимо так:
Первый слой - 5 нейронов по 5 синапсов
Второй слой - 5 нейронов по 5 синапсов
Выходной - нейрон с 5 синапсами.
Синапсов смещения нет.
Только я не понял, у нейросети 5 входов?

Все равно я не понял. По идее, модель НС как на картинке ниже. Но тут же 35 синапсов, без учета смещения?

(реклама)

Рисовал на https://gevaraweb.github.io/nndrawable/index2.html

Аа, вы наверное 25 связей два раза посчитали ))

[sergey zhukov]

gevaraweb
У меня такая сеть:

Я хочу аппроксимировать функцию от пяти переменных. Каждая переменная подается на каждый из пяти нейронов первого слоя.

[gevaraweb]

sergey zhukov в сообщении #1657318 писал(а):

Я хочу аппроксимировать функцию от пяти переменных.

Аааа. Нас с Mihaylo ввело в заблуждение:

sergey zhukov в сообщении #1657111 писал(а):

Сегодня решил попробовать научить нейронную сеть аппроксимировать функцию одной переменной.

[sergey zhukov]

gevaraweb
Да, это я что-то вначале не то написал. Хотел сказать, что у сети один выход.

[sergey zhukov]

Я разобрался, что у меня было. У меня в наборе всего 20 примеров. При начальной инициализации весов сеть дает некоторую ненулевую среднюю ошибку по всем этим примерам. Часто она вначале ошибается даже просто в одну и ту же сторону на всех примерах. Пока каждый пример требует корректировать веса в одну и ту же сторону, снижение ошибки идет быстро. Но как только средняя по всем примерам ошибка стала равной нулю, дальнейшее снижение ошибки происходит гораздо медленнее. Если отложить эволюцию ошибки сети каждого из 20 примеров в процессе обучения, то получим:

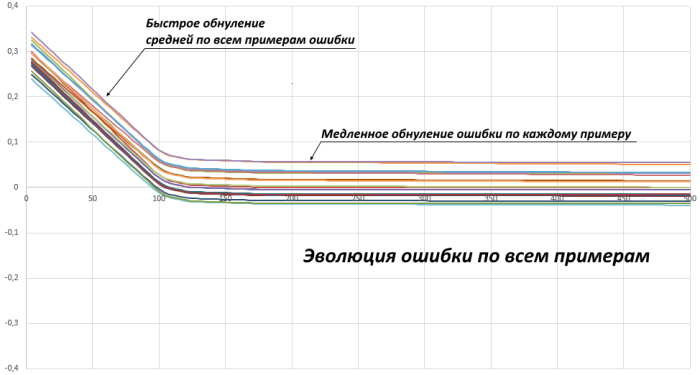
В данном случае тут не квадрат ошибки и не модуль, а просто разность ответа сети и правильного ответа. Меня сбило с толку, что скорость обучения вначале хорошая, но вдруг резко снижается.

Еще раз напишу, как я делал обучение.

Есть пример с правильным ответом $A_T$. Сеть дает ответ $A$. После изменения одного из ее весов $w_i$ на малый $\Delta w_i$ (постоянный параметр на всем обучении) она на этом же примере дает ответ $A^\prime$.

Абсолютная ошибка ответа $A$ сети есть $err=\left\lvert A_T-A \right\rvert$

Абсолютная ошибка ответа $A^\prime$ сети есть $err=\left\lvert A_T-A^\prime \right\rvert$

Ошибка изменилась на $\Delta err=err-err^\prime$

Нужно, чтобы подстройка веса приводила к $\Delta err>0$

Тогда нужно подстраивать вес так: $w_i^\prime=w_i+\alpha \Delta err$

На каждом примере сначала по очереди "дергаются" все веса, затем они все вместе корректируются (на данном примере).

Я заметил, что обучение лучше работает, если вместо $\Delta err=err-err^\prime$ брать $\Delta \overline{err}=err^2-{err^\prime}^2$, т.е. $w_i^\prime=w_i+\alpha \Delta \overline{err}$

А так обучение в общем работает нормально. Заданную функцию приближает хорошо (при удачном подборе параметров обучения). Пакетное обучение я попробую позже.

Такой вопрос возникает. У аппроксимируемой функции всего 5 параметров. А у этой сети 55 весовых коэффициентов. Явно избыточно. Но ведь и 5 весов будет явно недостаточно? Как примерно соотносится количество параметров аппроксимируемой функции и число весов сети?

[sergey zhukov]

Так примерно обучение происходит (кривые ошибки по всем примерам в процессе обучения) для функции $F=F(A,B,C,D,E)$:

Проще всего выучить линейную функцию, сложнее всего выучить случайную функцию (ответ не связан с входными данными). Также можно включить в множество примеров противоречивые примеры (функция от одного и того же аргумента имеет разное значение в разных примерах). Это выучить, разумеется, не получится.

Я так понял, что сеть в итоге способна выучить даже случайную функцию, но на это потребуется много итераций и большой размер сети. Например, в моем случае c 20 примерами по 6 параметров в каждом ей придется заучить $20*6=120$ независимых параметров (что слишком много для нее), если не учитывать какие-то случайные корреляции между ними.

Еще вроде бы получается, что сходимость обучения не гарантирована? Т.е. по крайней мере при упорядоченном предъявлении всех примеров по кругу не исключено, что можно попасть в ситуацию, когда ошибка на каждом примере падает при подстройке весов на нем и возвращается обратно при подстройке весов на всем остальном множестве примеров? Поэтому нужен малый шаг:

mihaild в сообщении #1657118 писал(а):

Обучение по одному примеру будет работать только при довольно малом шаге

[Mihaylo]

sergey zhukov в сообщении #1657323 писал(а):

Хотел сказать, что у сети один выход.

Вы так и сказали. Но у вас 5 входов.

[gevaraweb]

sergey zhukov в сообщении #1657362 писал(а):

Еще вроде бы получается, что сходимость обучения не гарантирована? ... Поэтому нужен малый шаг:

Ну да, либо пробовать быстро, но может не сойтись, либо будет сходится, но медленно.

А почему взяли сразу функцию 5 переменных? Может попробовать с 1 переменной?
Можно ли провести тогда вычисления вручную, например, 3-4 итераций, чтобы убедиться, что процесс сходится?
Для учебных целей потом использовать.

[sergey zhukov]

Функцию одной переменной я пробовал. Брал эту же сеть и пробовал два разных случая: либо подавал на все 5 входов одну и ту же переменную, либо подавал переменную только на первый вход, а на остальные входы подавал нули. Вот что получается:

Отсюда можно вроде бы сделать вывод, что для простой функции лучше "обнулить" лишние веса, чтобы они не вносили разброд в процесс обучения. А для сложной функции наоборот, обнуление большого числа весов может привести к "переупрощению" сети, и процесс обучения затянется.

Процесс в общем всегда сходится так или иначе, тут практических вопросов вроде нет. Единственно, что я четко не понял пока, так это как вычислять градиент. Я беру тут фиксированное приращение $\Delta w_i$ для всех весов при вычислении градиента, но можно ведь брать и не фиксированное приращение, адаптивное, разное для разных весов.

[gevaraweb]

sergey zhukov в сообщении #1657318 писал(а):

Я хочу аппроксимировать функцию от пяти переменных. Каждая переменная подается на каждый из пяти нейронов первого слоя.

Кстати, если добавить нейроны смещения, вдруг процесс обучения пойдет лучше?

Это что же получается, можно взять любой закон из физики, с 5 величинами, и нагенерировать кучу датасетов и учебных задач на тему регрессии? Которые имеют физическообразный смысл. Ну и добавлять погрешности измерения к каждой величине.
И у меня будет 30 вариантов для студентов . А то я как раз ищу способ, чтоб они не передавали друг другу и не отправляли все одно и то же решение submission.csv.
Я почему то думал, это делается какими то умными алгоритмами. Видимо, это верно для задач типа "Космический Титаник".

sergey zhukov в сообщении #1657339 писал(а):

У аппроксимируемой функции всего 5 параметров.

Вы опять оговорились, и имели в виду 5 переменных?
А то я мозг себе сломал, представляя функцию от 5 переменных с 5 параметрами.

[sergey zhukov]

gevaraweb в сообщении #1658326 писал(а):

Вы опять оговорились, и имели в виду 5 переменных?

Нет, я имел ввиду именно 5 параметров. Это просто случайно тут совпало с числом переменных.

Аппроксимируемая функция имеет какое-то число параметров, а сеть имеет какое-то число весов. Ясно, что у нас тут не просто преобразование переменных, число весов должно быть больше. Вот насколько больше, это интересно.