полная система вычетов?

[maxal]

Пусть $N=2^{127}-1$. Докажите или опровергните, что числа $\sum_{i=0}^{126} \alpha_i 5^i$, где $\alpha_i \in \{0,1\}$, представляют каждый вычет по модулю $N$ хотя бы раз.

[waxtep]

Можно понаблюдать за более скромными $N$, например, для $N=2^7-1$ выяснится, что $5^0+5^1+5^4+5^6\equiv0\pmod{N}$, и, значит, результат будет одинаковым, если разместить нули или единички на соответствующих местах, и полной системы вычетов не получится. Аналогично, для $N=2^8-1, 5^1+5^4+5^5+5^6\equiv0\pmod{N}$. Если удастся подобную сумму и для заданного $N=2^{127}-1$ построить, то докажем, что полной системы не будет

-- 30.05.2024, 22:56 --

Или, ещё более хитрый вариант для $N=2^9-1$, там $5^5+5^7\equiv5^0\pmod{N}$, и значит единичка в нулевой позиции эквивалентна единичкам в пятой и седьмой

-- 30.05.2024, 23:21 --

$N=2^{13}-1:5^2+5^4+5^5\equiv5^0+5^3+5^6+5^7\pmod{N}$. В общем, есть ощущение, что "всегда можно что-то намутить"

[maxal]

waxtep в сообщении #1640791 писал(а):

Если удастся подобную сумму и для заданного $N=2^{127}-1$ построить, то докажем, что полной системы не будет

Мне это не удалось, но было бы интересно увидеть такое вычислительное решение, если кто-то сумеет его построить.
Однако, у задачи есть решение без использования компьютера.

[Vadim32]

Есть такой вариант. Мы сравниваем два множества. Первое множество это множество всех вычетов N. Второе множество, это множество всех вычетов полученных из каждого полинома разрядности 127 с основанием 5. Так как основание простое число, то работаем в поле вычетов основания. Количество элементов второго множества на единицу больше, чем количество элементов всех вычетов. Для сравнения множеств будем использовать две контрольные суммы. В качестве первой суммы мы используем просто сумму всех элементов. Если множества отличаются только на один элемент, разница между суммой первого и суммой второго множества будет показывать какой элемент входит в состав второго множества дважды. Второй контрольной суммой можно использовать сумму квадратов каждого элемента. Разница в этом случае покажет квадрат лишнего элемента, входящего дважды во второе множество. Если квадрат лишнего элемента найденного как разницу первых контрольных сумм даст разницу между вторым контрольными суммами, то это подтвердит(но не докажет) гипотезу о том, что второе множество отличается от первого единственным лишним элементом. Но если гипотеза не подтвердится, то это доказывает что, множества отличаются более чем на один элемент, и не для каждого вычета существует соответствующий полином. Именно это демонстрирует программа.
Запустив программу можно посмотреть результат

127: N=170141183460469231731687303715884105727
poly_sum1=80280682861595619370168968130363211378
sum1=0
d1=80280682861595619370168968130363211378
poly_sum2=155729045835901150045551746619023564571
sum2=0
d2=155729045835901150045551746619023564571
d2-d1*d1=31765023455761517083774786768884716470
Error!

Программой можно подтвердить равенство для 2 и 3 бит. Для 6 бит подтверждение ложное. Для остальных битностей равенство не подтверждается.

Используется синтаксис C++

#include <iostream>
#include <boost/multiprecision/cpp_int.hpp>
using namespace std;
using namespace boost::multiprecision;

template <class T>
T calculate_sum1(T max_value)
{
   return  max_value*(max_value+1)/2;
}

template <class T>
T calculate_sum2(T max_value)
{  T s1=max_value;
   T s2=s1*max_value;
   T s3=s2*max_value;
   return  (max_value + 3*s2 + 2*s3)/6;
}

template <class T, int BASE>
class BINARY_POLY
{ 
public:
   const int NBIT;
   const T NITEMS;
   const T N;
   T *digit;

   BINARY_POLY(int nbit):NBIT(nbit),NITEMS(pow((T)2,nbit)), N(NITEMS-1), digit(new T[nbit]) 
   {  T d=1;
      for(int nb=0; nb<NBIT; nb++)
      {  digit[nb]=d;
         d=(d*BASE) % N;
      }
   }
   ~BINARY_POLY()
   {  delete digit;
   }

   T calculate_sum1(int ndigits)
   {  
      T digit_sum=0;
      for(int nb=0; nb<ndigits; nb++)
      { 
         digit_sum+=digit[nb];
      }
      T number_of_items=pow((T)2, ndigits-1);

      return ((digit_sum % N)  * number_of_items) % N;
   }

   T calculate_sum1()
   {  return calculate_sum1(NBIT);
   }

   T calculate_sum2(int ndigits)
   {  
      if (ndigits==1)  
      {  return 1;
      }
      else
      {  T n_items=pow((T)2,ndigits-1);
         T d=digit[ndigits-1];
         T s1=calculate_sum1(ndigits-1);
         T s2=calculate_sum2(ndigits-1);
         T S =  ((d*d)% N)*n_items + (2*d*s1  +   s2  + s2);

         return S % N;
      }
   }
   
   T calculate_sum2()
   {  return calculate_sum2(NBIT);
   }
};


int main(int argc, char* argv[])
{
   for(int nb=127; nb<128; nb++)
   {  
      typedef uint512_t T;
      BINARY_POLY<T,5> poly(nb);
      cout << nb << ": " << "N="<< poly.N<< endl; 
      
      T sum1=calculate_sum1(poly.N-1)  % poly.N;
      T poly_sum1=poly.calculate_sum1();
      T delta_sum1=(poly_sum1  + poly.N - sum1) % poly.N;
      cout << " poly_sum1=" << poly_sum1 << endl;
      cout << " sum1=" << sum1 << endl;
      cout << " d1=" << (poly_sum1 + poly.N - sum1) % poly.N <<endl;

      T sum2=calculate_sum2(poly.N-1) % poly.N;
      T poly_sum2=poly.calculate_sum2();
      T delta_sum2=(poly_sum2 + poly.N - sum2) % poly.N;
      cout << " poly_sum2=" << poly_sum2 << endl;
      cout << " sum2=" << sum2 << endl;
      cout << " d2=" << (poly_sum2 + poly.N - sum2) % poly.N <<endl;
      
      T d=((delta_sum1*delta_sum1) % poly.N  + poly.N - delta_sum2) % poly.N;
      cout << " d2-d1*d1=" << d <<endl;
      cout << (d? " Error!" : " No error found") ;
      cout << endl << endl;
   }
        return 0;
}

[maxal]

Vadim32
Перефразируя ваш текст, вы тестируете сравнение

$$\sum_{\alpha\in\{0,1\}^{127}} (\sum_{i=0}^{126} \alpha_i 5^i)^2 \equiv \big(\sum_{\alpha\in\{0,1\}^{127}} \sum_{i=0}^{126} \alpha_i 5^i\big)^2 \pmod N.$$

Нетрудно видеть, что правая часть это просто

$$\big( \frac{5^{127}-1}8\big)^2 \pmod N,$$

а левая часть раскрывается в

$$\sum_{\alpha\in\{0,1\}^{127}} \sum_{i,j=0}^{126} \alpha_i\alpha_j 5^{i+j} \equiv \frac14 \sum_{i,j=0\atop i\ne j}^{126} 5^{i+j} + \frac12 \sum_{i=0}^{126} 5^{2i} \equiv \big( \frac{5^{127}-1}8\big)^2 + \frac{5^{254}-1}{96}\pmod N.$$

Так как $\frac{5^{254}-1}{96}\not\equiv 0\pmod N$, то ответ на вопрос задачи отрицательный.

Однако, ваше значение d2-d1*d1=31765023455761517083774786768884716470 не совпадает с $\frac{5^{254}-1}{96}\bmod N = 138376160004707714647912516946999389257$. Ищите ошибку в своем коде.

[Vadim32]

Да, пишу одно, делаю другое, отсюда и знак минус потерян.
вот исправление

Используется синтаксис C++

int main(int argc, char* argv[])
{
   for(int nb=127; nb<128; nb++)
   {  
      typedef uint512_t T;
      BINARY_POLY<T,5> poly(nb);
      cout << nb << ": " << "N="<< poly.N<< endl; 
      
      T sum1=calculate_sum1(poly.N-1)  % poly.N;
      T poly_sum1=poly.calculate_sum1();
      T delta_sum1=(poly_sum1  + poly.N - sum1) % poly.N;
      cout << " poly_sum1=" << poly_sum1 << endl;
      cout << " sum1=" << sum1 << endl;
      cout << " d1=" << delta_sum1 <<endl;

      T sum2=calculate_sum2(poly.N-1) % poly.N;
      T poly_sum2=poly.calculate_sum2();
      T delta_sum2=(poly_sum2 + poly.N - sum2) % poly.N;
      cout << " poly_sum2=" << poly_sum2 << endl;
      cout << " sum2=" << sum2 << endl;
      cout << " d2=" << delta_sum2 <<endl;
      
      //T d=((delta_sum1*delta_sum1) % poly.N  + poly.N - delta_sum2) % poly.N;
      T d=(delta_sum2 + poly.N - (delta_sum1*delta_sum1) % poly.N   ) % poly.N;
      cout << " d2-d1*d1=" << d <<endl;
      cout << (d? " Error!" : " No error found") ;
      cout << endl << endl;
   }
        return 0;
}

и вот результат:

127: N=170141183460469231731687303715884105727
poly_sum1=80280682861595619370168968130363211378
sum1=0
d1=80280682861595619370168968130363211378
poly_sum2=155729045835901150045551746619023564571
sum2=0
d2=155729045835901150045551746619023564571
d2-d1*d1=138376160004707714647912516946999389257
Error!


Но всё же я не только тестирую сравнения, я ещё и вычитаю суммы первого множества. Понятно, что сумма вычетов всегда даст ноль для простого числа, но вот сумма квадратов, как-то не очевидно - всегда ли будет ноль, думаю нет.

[maxal]

Vadim32 в сообщении #1641111 писал(а):

но вот сумма квадратов, как-то не очевидно - всегда ли будет ноль, думаю нет

Будет, как и для любой другой степени не кратной $p-1$. Это легко вывести из существования первообразного корня по модулю $p$.

[lel0lel]

Без компьютера)
$p=127, N=2^p-1\in \mathbb{P}$. Определяются множества: $A=\{\sum_{i=1}^{p-1} \alpha_i 5^i \bmod N \mid \alpha_i \in\{0,1\}\}$, $B=\{ (1+a) \bmod N \mid a\in A\}$. Это множества вычетов, полученные из исходных чисел, имеющих $\alpha_0=0$ и $\alpha_0=1$, соответственно. Нетрудно видеть что
1. если $a\in A$, то $a+1\in B$
2. если $b\in B$, то $b-1\in A$
Тогда полная система вычетов образуется только если упорядоченные остатки исходных чисел образуют следующую "структуру":
$\{A,B,A,B,\ldots,A,(B,A),B,A,\ldots,B\}$, что соответствует $\{0,1,2,3,\ldots,y-1,(y,y),y+1,y+2,\ldots,N-1\}$, при этом $|A|=|B|=2^{p-1}$, $|A\cap B|=1$. Здесь $(B,A)$ означает, что два исходных различных числа попадают в один класс вычетов $y$. Позиция $(B,A)$ в списке пока неизвестна, в принципе, это может быть первый элемент списка ($y=0$), а вот последним быть не может (иначе первый элемент тоже пара). Также понятно, что никаких $(A,A)$ в списке быть не может, по причине последующих за ними $(B,B)$. В общем-то, $y$ выше уже находили через сумму всех чисел, но можно и так: пара $(A,B)$ только в том случае не "сгенерирует" другие пары $(A,B)$, если в числах, из которых она получена, нули и единички проживают в несовпадающих позициях. Поэтому $2y\equiv \sum_{i=0}^{p-1}5^i \equiv\frac{5^p-1}{4}\pmod N$. Значение $y$ без компьютера не вычислить, поэтому нужно обратить внимание на обсуждаемую "структуру". Если идти в ней по возрастанию вычетов, принадлежащих $A$, то чётность вычетов меняется только один раз, это происходит на вычете $y$. С другой стороны, в нашем случае есть немало представителей $A$ различной чётности: $0,5,30,125,130,155...$ Следовательно, как минимум четыре вычета полной системы вычетов получить нельзя.

[waxtep]

maxal в сообщении #1640813 писал(а):

Мне это не удалось, но было бы интересно увидеть такое вычислительное решение, если кто-то сумеет его построить.

Вернулся к этой задаче: найти какое-либо разложение натурального $N=2^n-1$ в сумму натуральных степеней пятерок с коэффициентами $\{-1,0,1\}$. Добраться мне пока удалось до заметно более скромного 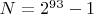$N=2^{93}-1$:

(21:33) gp > q1=5^92+5^89+5^84+5^79+5^59+5^57+5^56+5^49+5^44+5^43+5^42+5^38+5^19+5^17+5^14+5^13+5^12+5^9+5^6+5^3+1
%66 = 20356449602379062251578988040918723300273995846509953315675797001
(21:33) gp > q2=5^81+5^71+5^69+5^67+5^65+5^62+5^61+5^58+5^55+5^46+5^21+5^20+5^5+5^2+5
%63 = 413590350392726291695044835705630248412490463256835940655
(21:34) gp > q=q1-q2
%67 = 20356449188788711858852696345873887594643747434019490058839856346
(21:34) gp > q/(2^93-1)
%68 = 2055476087571634518751370354306509606

При помощи такого рецепта:
1. берем упорядоченную по убыванию последовательность остатков 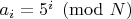$a_i=5^i\pmod{N}$, добавляем к ней и само $N$;
2. вычисляем разности соседей 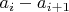$a_i-a_{i+1}$ и может быть какие-нибудь еще комбинации из $a_i$, и вставляем их обратно в упорядоченную последовательность; проверяя отсутствие полных дубликатов и "запрещенных" комбинаций с коэффициентом по модулю большим единицы при какой-нибудь степени пятерки;
3. повторяем предыдущий шаг в цикле; по наблюдениям, дюжины итераций хватает, чтобы алгоритм завершился успехом или поражением.

Конкретно для $n=93$ на шаге 2 беру разности 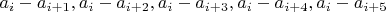$a_i-a_{i+1},a_i-a_{i+2},a_i-a_{i+3},a_i-a_{i+4},a_i-a_{i+5}$; это считается минут 45 на древнем офисном нотике; наибольшее количество членов $a_i$ - 48776 - получается на пятой итерации, а всего итераций десять штук.
Для $n=86$ можно не брать последнюю из комбинаций; а для $n$ в районе $40$ достаточно первых одной-двух комбинаций. В общем, есть ощущение, что необходимое количество комбинаций увеличивается с ростом $n$.

На этом месте хочется остановиться, и обсудить пару вопросов, если кого-либо из участников заинтересует тема:
1. Почему это работает? Всего комбинаций для 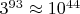$n=93$ порядка $3^{93}\approx10^{44}$, а перебрать достаточно сотню тысяч. Это просто везение, или есть какие-то правдоподобные соображения или даже теория? Да, мы на каждой итерации добавляем точки и сжимаем интервал, но разница в $39$ десятичных порядков так сказать вопиет

2. Если соображения есть, можно ли как-то более интеллектуально подобрать вид комбинаций, чтобы обойтись их меньшим числом? От их количества время расчета зависит ощутимо.

3. Сколько времени этот код исполняется на нормальных машинах, и где бы его пооптимизировать. Это же просто задача вставки в отсортированный массив, ну в моем топорном исполнении.

Код:

1. f52n(n)={ 
2. \\try to find a multiple of N=2^n-1 as a sum of b[i]*5^i, i=0,1,...,n-1, b[i]=-1,0,1 
3. N=2^n-1; 
4. a=vector(n,i,lift(Mod(5^(n-i),N))); 
5. a=matconcat([N,a]); 
6. s=vector(n,i,[n-i+1]); 
7. s=matconcat([n+1,s]); 
8. \\each a[k]=g[2,k] is some sum of b[i]*5^i mod N, a building block for desirable multiple; ordered desc 
9. \\corresponding g[1,k] is a set of integers s[j] storing a formula for g[1,n]: g[1,n]=sum(sign(s[j])*5^(abs(s[j]-sign(s[j])))), where abs(s[j])<n+1 
10. \\s[j]=n+1 is reserved for g[1,k]=N and should be ignored in the output 
11. \\example: n=9, s=[-10, -2, 7, 9] => a=5^8+5^6-5^1 
12. g=matconcat([s,a]~); 
13. g[1,1]=Set(g[1,1]); 
14. g=vecsort(g,2,4); 
15.  
16. \\basically, while(1); commonly runs for no more than a dozen iterations 
17. for(ecnt=1,1000, 
18. w=#g-1; 
19. c=[]; 
20. mnmax=0; 
21. for(cnt=1,w, 
22. c1=g[1,cnt]; 
23.  
24. \\main job is done here; calculate "good" a[k]-a[k+1] and insert them back into ordered vector g[2,...] 
25. \\or return first suitable g[1,k] that yields a multiple of N 
26. \\need to check here that we are not trying to insert some 2*5^i here 
27. c2=g[1,cnt+1]; 
28. if(setintersect(c1,vecsort(-c2))==[],cn=vecsort(setunion(setminus(c1,c2),-setminus(c2,c1))); 
29. mn=g[2,cnt]-g[2,cnt+1];  
30. \\also avoid inserting duplicate g[1,k] 
31. ndup=vecsearch(-g[2,1..w],-mn); 
32. if(ndup>0,if(g[1,ndup]!=cn && setintersect(vecsort(-cn),g[1,ndup])==[],return(matconcat([-cn,g[1,ndup]])))); 
33. if(ndup==0, 
34. if(c==[] && mn==0, return(cn)); 
35. if(c==[],mnmax=mn;c=[cn;mn]); 
36. cdup==0; 
37. if(c!=[],cdup=vecsearch(-c[2,1..#c],-mn);if(cdup>0 && cn!=c[1,cdup] && setintersect(vecsort(-cn),c[1,cdup])==[],print("new");return(vecsort(setunion(setminus(cn,c[1,cdup]),-setminus(c[1,cdup],cn)))))); 
38. if(cdup==0, 
39. if(mn>mnmax,mnmax=mn); 
40. if(c==[],c=[cn;mn],c=vecsort(matconcat([[cn;mn],c]),2,4))))); 
41.  
42. \\same as above for a[k]-a[k+2] 
43. if(cnt<w, 
44. c2=g[1,cnt+2]; 
45. if(setintersect(c1,vecsort(-c2))==[],cn=vecsort(setunion(setminus(c1,c2),-setminus(c2,c1))); 
46. mn=g[2,cnt]-g[2,cnt+2];  
47. ndup=vecsearch(-g[2,1..w],-mn); 
48. if(ndup>0,if(g[1,ndup]!=cn && setintersect(vecsort(-cn),g[1,ndup])==[],return(matconcat([-cn,g[1,ndup]])))); 
49. if(ndup==0, 
50. if(c==[] && mn==0, return(cn)); 
51. if(c==[],mnmax=mn;c=[cn;mn]); 
52. cdup==0; 
53. if(c!=[],cdup=vecsearch(-c[2,1..#c],-mn);if(cdup>0 && cn!=c[1,cdup] && setintersect(vecsort(-cn),c[1,cdup])==[],print("new1");return(vecsort(setunion(setminus(cn,c[1,cdup]),-setminus(c[1,cdup],cn)))))); 
54. if(cdup==0, 
55. if(mn>mnmax,mnmax=mn); 
56. if(c==[],c=[cn;mn],c=vecsort(matconcat([[cn;mn],c]),2,4))))); 
57. ); 
58.  
59. \\same as above for a[k]-a[k+3] 
60. if(cnt<w-1, 
61. c2=g[1,cnt+3]; 
62. if(setintersect(c1,vecsort(-c2))==[],cn=vecsort(setunion(setminus(c1,c2),-setminus(c2,c1))); 
63. mn=g[2,cnt]-g[2,cnt+3];  
64. ndup=vecsearch(-g[2,1..w],-mn); 
65. if(ndup>0,if(g[1,ndup]!=cn && setintersect(vecsort(-cn),g[1,ndup])==[],return(matconcat([-cn,g[1,ndup]])))); 
66. if(ndup==0, 
67. if(c==[] && mn==0, return(cn)); 
68. if(c==[],mnmax=mn;c=[cn;mn]); 
69. cdup==0; 
70. if(c!=[],cdup=vecsearch(-c[2,1..#c],-mn);if(cdup>0 && cn!=c[1,cdup] && setintersect(vecsort(-cn),c[1,cdup])==[],print("new2");return(vecsort(setunion(setminus(cn,c[1,cdup]),-setminus(c[1,cdup],cn)))))); 
71. if(cdup==0, 
72. if(mn>mnmax,mnmax=mn); 
73. if(c==[],c=[cn;mn],c=vecsort(matconcat([[cn;mn],c]),2,4))))); 
74. ); 
75.  
76. \\same as above for a[k]-a[k+4] 
77. if(cnt<w-2, 
78. c2=g[1,cnt+4]; 
79. if(setintersect(c1,vecsort(-c2))==[],cn=vecsort(setunion(setminus(c1,c2),-setminus(c2,c1))); 
80. mn=g[2,cnt]-g[2,cnt+4];  
81. ndup=vecsearch(-g[2,1..w],-mn); 
82. if(ndup>0,if(g[1,ndup]!=cn && setintersect(vecsort(-cn),g[1,ndup])==[],return(matconcat([-cn,g[1,ndup]])))); 
83. if(ndup==0, 
84. if(c==[] && mn==0, return(cn)); 
85. if(c==[],mnmax=mn;c=[cn;mn]); 
86. cdup==0; 
87. if(c!=[],cdup=vecsearch(-c[2,1..#c],-mn);if(cdup>0 && cn!=c[1,cdup] && setintersect(vecsort(-cn),c[1,cdup])==[],print("new3");return(vecsort(setunion(setminus(cn,c[1,cdup]),-setminus(c[1,cdup],cn)))))); 
88. if(cdup==0, 
89. if(mn>mnmax,mnmax=mn); 
90. if(c==[],c=[cn;mn],c=vecsort(matconcat([[cn;mn],c]),2,4))))); 
91. ); 
92.  
93. \\same as above for a[k]-a[k+5] 
94. if(cnt<w-3, 
95. c2=g[1,cnt+5]; 
96. if(setintersect(c1,vecsort(-c2))==[],cn=vecsort(setunion(setminus(c1,c2),-setminus(c2,c1))); 
97. mn=g[2,cnt]-g[2,cnt+5];  
98. ndup=vecsearch(-g[2,1..w],-mn); 
99. if(ndup>0,if(g[1,ndup]!=cn && setintersect(vecsort(-cn),g[1,ndup])==[],return(matconcat([-cn,g[1,ndup]])))); 
100. if(ndup==0, 
101. if(c==[] && mn==0, return(cn)); 
102. if(c==[],mnmax=mn;c=[cn;mn]); 
103. cdup==0; 
104. if(c!=[],cdup=vecsearch(-c[2,1..#c],-mn);if(cdup>0 && cn!=c[1,cdup] && setintersect(vecsort(-cn),c[1,cdup])==[],print("new4");return(vecsort(setunion(setminus(cn,c[1,cdup]),-setminus(c[1,cdup],cn)))))); 
105. if(cdup==0, 
106. if(mn>mnmax,mnmax=mn); 
107. if(c==[],c=[cn;mn],c=vecsort(matconcat([[cn;mn],c]),2,4))))); 
108. ); 
109.  
110.  
111. ); 
112. \\failure: no more candidates for insert 
113. if(c==[],print(ecnt);return([]),g=matconcat([c,g])); 
114.  
115. \\remove too large a[k] - no new candidates here 
116. g=vecsort(g,2,4); 
117. w=#g; 
118. wcut=vecsearch(-g[2,1..w],-mnmax); 
119. g=g[1..2,wcut..w]; 
120. print(#g); 
121. ); 
122.  
123. }; 

Пример запуска и выдача (размер последовательности на каждой итерации и найденное разложение):

(20:33) gp > f52n(93)
502
1942
7589
25489
  *** vecsort: Warning: increasing stack size to 128000000.
48776
47486
24041
5144
2066
1155
%61 =
[93 90 85 80 60 58 57 50 45 44 43 39 20 18 15 14 13 10 7 -6 -21 -22 -47 -56 -59 -62 -63 -66 -68 -70 -72 -82 -94 -3 -2 1 4]

[waxtep]

Для $N=2^{127}-1$ программа считает почти три часа и ничего не находит:

(00:14) gp > f52n(127)
683
2631
10912
38607
  *** vecsort: Warning: increasing stack size to 128000000.
  *** vecsort: Warning: increasing stack size to 256000000.
80040
74732
28290
5978
2681
1618
932
559
440
413
15
%196 = []

[waxtep]

Можно преодолеть психологический барьер в сотню и "поймать" $N=2^{101}-1$, добавив в поиск шестую комбинацию типового вида $a_n-a_{n+6}$:

(18:57) gp > f52n(101)
[0, 102, 2535301200456458802993406410750]
[1, 643, 451659283795258692593506560683]
[2, 2942, 79582891105463062204368698076]
[3, 13541, 4583415235064913640841387800]
  *** vecsort: Warning: increasing stack size to 128000000.
[4, 53838, 57244015419772958892964768]
  *** vecsort: Warning: increasing stack size to 256000000.
[5, 114386, 333366927876147102719768]
[6, 101344, 919016828805020751872]
[7, 45792, 866123028189714880]
[8, 10048, 147030293138321]
[9, 4136, 177039241862]
%625 =
[93 88 74 57 55 49 43 30 29 26 25 19 18 16 15 14 8 7 -5 -6 -9 -12 -13 -21 -22 -23 -24 -28 -32 -51 -61 -76 -80 -84 -85 -90 -2 -1 3 4]

(10:37) gp > r=%625;
(10:44) gp > q=vecsum(vector(#r,j,sign(r[1,j])*5^(abs(r[1,j]-sign(r[1,j])))))
%630 = 20039680753689244812947198359690759389195586771115689124462590144
(10:44) gp > q/(2^101-1)
%631 = 7904260349847692887577806012942144

(я немного дополнил вывод, добавил к количеству точек номер итерации и ширину диапазона, в котором идет поиск). В человеческом виде это означает

$$5^{92}+5^{87}+\ldots+5^3+5^2-(5^{89}+5^{84}+\ldots+5+1)=7\,904\,260\,349\,847\,692\,887\,577\,806\,012\,942\,144\,\times\,(2^{101}-1)$$

Шесть комбинаций в поиске это видимо предел достижимого на моей слабой тачке, $n=101$ считалось почти шесть часов.

Что касается чуть более интеллектуального подхода: кажется осмысленным добавить к исходной последовательности остатков не только $N$, но и максимальное кратное $N$, которое еще можно сложить из остатков. Текущий алгоритм пытается сложить из остатков $0$ или $N$, но можно ведь попытать счастье и с $2N,3N,\ldots$. Это потребует некоторой нудной реорганизации кода, поскольку такие нули по модулю $N$ имеют право дублироваться; на выходных попробую

[Yadryara]

Начинаю знакомиться с темой. Числа Мерсенна.

Правильно ли я понимаю, что для $N=7$ ПСВ как раз есть?

№   Nabor             s   s%N  Comment

1   []                0     0
2   [1]               1     1
3   [1, 0]            5     5        1
4   [1, 1]            6     6
5   [1, 0, 0]        25     4
6   [1, 0, 1]        26     5        2
7   [1, 1, 0]        30     2
8   [1, 1, 1]        31     3

[lel0lel]

Yadryara в сообщении #1699171 писал(а):

Правильно ли я понимаю, что для $N=7$ ПСВ как раз есть?

Правильно.

Waxter в сообщении #1699171 писал(а):

Можно преодолеть психологический барьер в сотню и "поймать" $N=2^{101}-1$

Я немного другой способ применил: проверял представления в пятеричной системе остатков различных комбинаций $\pm5^{i_1}\pm5^{i_2}\pm5^{i_3}\pm5^{i_4}\pm\ldots$, где $i_1,i_2,i_3,i_4,\ldots>\log_5 N$. Нетрудно описать, какие остатки нам подходят, чтобы их было легко разложить в комбинацию слагаемых вида $\pm5^k$, где показатели степеней меньше $\log_5 N$. Понятно, что двоек в разложении быть не должно, тройка быть может, но только в таком "окружении" $\{0,3,4\},3,\{3,4\}$ (в фигурных скобках указаны возможные соседние цифры справа-слева). Цифра четыре может появляться в таком окружении $\{0,3,4\},4,\{0,1,3,4\}$. В общем, остатков подходящего вида немало и, судя по опытам, искомых представлений тоже много. Дальше небольшой рандом с запуском на двух ядрах. Примерно через пару часов нашлось:

Mod[5^83 + 5^61 + 5^39 + 5^38 + 5^35 + 5^34 + 5^33 + 5^31 + 5^25 + 5^24 + 5^23 + 5^16 + 5^11 + 5^7 + 5^2 + 5^0 
- 5^91 - 5^88 - 5^86 - 5^78 - 5^75 - 5^57 - 5^56 - 5^50 - 5^41 - 5^26 - 5^22 - 5^21 - 5^13 - 5^12 - 5^10 - 5^6 - 5^4, 2^101 - 1]==0
True

[waxtep]

lel0lel, а Вам удалось дотянуться до $2^{127}-1$? Мне пока нет, но хотя бы код пооптимизировал, для $2^{101}-1$ находит (другое) решение за минуту:

1. f52isnice(a,b)={return(bitand(real(a),imag(b))==0 && bitand(real(b),imag(a))==0)}; 
2.  
3. f52diff(a,b)={my([L1,R1]=[real(a),imag(a)],[L2,R2]=[real(b),imag(b)],RC,LC,G); 
4. G=bitxor(bitand(L1,L2),bitand(R1,R2)); 
5. return(bitxor(G,bitor(L1,R2))+I*bitxor(G,bitor(L2,R1))) 
6. }; 
7.  
8. f52dec(s,n)={my( 
9. L=binary(real(s)), 
10. R=binary(imag(s)), 
11. L1=select(x->x,L,1), 
12. R1=select(x->x,R,1), 
13. L2=vector(#L1,i,#L-L1[i]), 
14. R2=vector(#R1,i,#R-R1[i]), 
15. r=(sum(i=1,#L2,5^L2[i])-sum(i=1,#R2,5^R2[i]))/(2^n-1); 
16. ); 
17. return([L2;R2;r]); 
18. }; 
19.  
20. f52nb(n,combo)={ 
21. \\try to find a multiple of N=2^n-1 as a sum of b[i]*5^i, i=0,1,...,n-1, b[i]=-1,0,1 
22. t0=getabstime(); 
23. N=2^n-1; 
24. a=vector(n,i,lift(Mod(5^(i-1),N))); 
25. k=floor(vecsum(a)/N); print(k); if(k<2,k=2); 
26. a=vector(n+1,i,if(i<n+1,a[i],N)); \\dunno a nice way for concating two vectors 
27. a=vector(n+2,i,if(i<n+2,a[i],k*N)); 
28.  
29. s=vector(n,i,2^(i-1)); 
30. s=vector(n+2,i,if(i<n+1,s[i],0)); 
31.  
32. \\pack b[i] into bits of a complex number: 5+2i => [101, 10] => 5^2+5^0-5^1 
33. aind=vecsort(a,,1); 
34. a=vecextract(a,aind); 
35. s=vecextract(s,aind); 
36. \\print(a); 
37. \\print(s); 
38.  
39. \\DD=7; \\max search depth 
40. DD=#combo; 
41.  
42. for(ecnt=1,max(30,k+15),\\basically while(1) 
43. wa=#a; 
44. anew=a; 
45. snew=s; 
46. wanew=wa; 
47.  
48. \\main job 
49. for(dcnt=1,DD, 
50. dep=combo[dcnt]; 
51. da=vector(wa-dep,i,if(f52isnice(s[i+dep],s[i]),a[i+dep]-a[i],-1)); 
52. ds=vector(wa-dep,i,if(f52isnice(s[i+dep],s[i]),f52diff(s[i+dep],s[i]),-1)); 
53. wda=#da; 
54.  
55. anew=vector(wanew+wda,i,if(i<=wanew,anew[i],da[i-wanew])); 
56. snew=vector(wanew+wda,i,if(i<=wanew,snew[i],ds[i-wanew])); 
57. wanew=#anew; 
58. ); \\end for dep 
59.  
60. g=matconcat([anew,snew]~); 
61. aind=vecsort(g,,9); \\remove full duplicates 
62. a=vecextract(anew,aind); 
63. s=vecextract(snew,aind); 
64. if(a[1]==-1,wa=#a;a=a[2..wa];s=s[2..wa]); \\remove one last bad combo s 
65. print(["===>",ecnt,#a]); 
66.  
67. if(a[1]==0,print(getabstime()-t0," ms");return(f52dec(s[1],n))); \\success 
68.  
69. ); \\end for ecnt 
70. print(getabstime()-t0," ms"); 
71. return([]); \\failure 
72. }; 

(01:55) gp > f52nb(101,[1,2,3,4,5,6])
25
["===>", 1, 700]
["===>", 2, 3261]
["===>", 3, 14702]
["===>", 4, 59175]
  *** matconcat: Warning: increasing stack size to 128000000.
["===>", 5, 142209]
  *** matconcat: Warning: increasing stack size to 256000000.
["===>", 6, 203730]
  *** matconcat: Warning: increasing stack size to 512000000.
["===>", 7, 238919]
["===>", 8, 265610]
["===>", 9, 273966]
["===>", 10, 276952]
["===>", 11, 277774]
57875 ms
%1045 =
[ [89, 84, 83, 79, 75, 60, 50, 31, 27, 23, 22, 21, 20, 12, 11, 8, 5, 4, 1, 0]]

[[92, 87, 73, 56, 54, 48, 42, 29, 28, 25, 24, 18, 17, 15, 14, 13, 7, 6, 3, 2]]

[                                         -7904260349847692887577806012942144]

Перешел на работу с векторами, а степени пятерки упаковал в биты комплексного числа. Код все равно кривой*, но все же минута заметно лучше шести часов
И, думаю, Вы правы: решений видимо немало, и даже самая дикая стратегия имеет шанс на решение наткнуться.

* - как минимум, в коде две проблемы: 1) он всегда перелопачивает весь массив комбинаций из остатков, что избыточно и прожорливо по памяти и 2) "экранировка" - когда рядом стоят два равных числа, и в представлении одного из них есть какое-то $+5^k$, а у другого $-5^k$; такие оседают мертвым грузом и потенциально пропускают решение. Обе проблемы, кажется, решает использование связанного списка вместо вектора, но это ж надо суметь реализовать его по-человечески

[lel0lel]

waxtep в сообщении #1699576 писал(а):

а Вам удалось дотянуться до $2^{127}-1$?

Нет. Не стану лукавить, что больше ночи на трёх ядрах я искал, но ничего не нашлось. Потом возникла идея набрать побольше остатков и покомбинировать их до нужного состояния. А потом я отвлёкся и подумал, что -- "а, ну и ладно"
Хочется заметить, что число простое. Для составных можно искать решения по каждому сомножителю.