полная система вычетов?

[Руст]

$N=p$ - простое число Мерсена. Учитывая, что $(\frac{5}{p})=(\frac{2^{127}-1}{5})=-1$,
получаем, что последовательность Люка с дискриминантом $5,20, 5*k^2$ имеет период $p+1=2^{127}$ (или делитель).
Дискриминант не обязательно должен быть 5 или 20. Достаточно, чтобы по модулю этого числа.
Так можно привести все вычеты к всем различным по модулю р числам Люка.

[maxal]

Руст в сообщении #1699664 писал(а):

$N=p$ - простое число Мерсена. Учитывая, что $(\frac{5}{p})=(\frac{2^{127}-1}{5})=-1$,
получаем, что последовательность Люка с дискриминантом $5,20, 5*k^2$ имеет период $p+1=2^{127}$ (или делитель).
Дискриминант не обязательно должен быть 5 или 20. Достаточно, чтобы по модулю этого числа.
Так можно привести все вычеты к всем различным по модулю р числам Люка.

Для меня это звучит как обрывки мыслей. Можно попросить чётко сформулировать утверждение?

[waxtep]

Есть!

8216578 ms
%65 =
[[117, 111, 110, 109, 105, 104, 99, 96, 89, 86, 79, 73, 70, 67, 60, 53, 52, 33, 31, 25, 22, 18, 4]]

[[121, 120, 116, 107, 103, 92, 85, 80, 77, 75, 68, 62, 61, 57, 48, 32, 29, 24, 23, 21, 20, 19, 17, 13, 12, 10, 9, 5, 3, 2]]

[-26502008000322474857503473393349650738225653825]

Можно еще на $25$ поделить конечно, и будет

$$5^{119}+5^{118}+\ldots+5+1-(5^{115}+5^{109}+\ldots+5^{16}+5^2)\equiv0\pmod{(2^{127}-1)}$$

lel0lel, воспользовался Вашей подсказкой и применил мощь рандома. Оно могло бы и за три минуты посчитаться (средняя длительность одной из независимых попыток), а могло к концу света, тут как повезет. Детали позже добавлю

[lel0lel]

waxtep
Отличный результат, поздравляю!

waxtep в сообщении #1699873 писал(а):

воспользовался Вашей подсказкой и применил мощь рандома. Оно могло бы и за три минуты посчитаться (средняя длительность одной из независимых попыток), а могло к концу света, тут как повезет

Не велика подсказка Всё-таки тут не любой алгоритм, основанный на рандоме, сработает. Вы последовательность множеств остатков, как я понял, по некоторым паттернам (правилам перехода к новым комбинациям) строите. Думаю, что угадать паттерн легче, чем угадывание больших степеней в представлении (это то, что использовал я). Вам стоит попробовать жадный алгоритм рандома, если какой-то паттерн за некоторое не очень большое время не даёт результат, сбрасывать его и запускать с новым. Хотя, я не очень вникал, возможно, что правила перехода Вы руками задаёте, а рандом по начальным данным. Какое там следующее простое Мерсенна?

[waxtep]

lel0lel в сообщении #1699896 писал(а):

Вы последовательность множеств остатков, как я понял, по некоторым паттернам (правилам перехода к новым комбинациям) строите. Думаю, что угадать паттерн легче, чем угадывание больших степеней в представлении (это то, что использовал я). Вам стоит попробовать жадный алгоритм рандома, если какой-то паттерн за некоторое не очень большое время не даёт результат, сбрасывать его и запускать с новым. Хотя, я не очень вникал, возможно, что правила перехода Вы руками задаёте, а рандом по начальным данным.

Да-да, в эту сторону я ходил: с некоторой долей случайности выбираются паттерны при каждом переходе, и сброс, если поиск слишком затянулся. Подробнее:

0. Делаем сколько-то независимых попыток, пока не надоест; я обычно двухсот не дожидался. В каждой попытке:
1. Начинаем с упорядоченной по возрастанию последовательности остатков 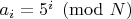$a_i=5^i\pmod{N}$, добавляем к ней еще два числа 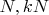$N,kN$, где 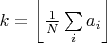$k=\left\lfloor\frac1N\sum\limits_i{a_i}\right\rfloor$
2. При каждом переходе для каждого $a_i$ вычисляем четыре (или меньше) разности 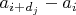$a_{i+d_j}-a_i$ и вставляем их обратно в упорядоченную последовательность; проверяя отсутствие полных дубликатов и "запрещенных" комбинаций с коэффициентом по модулю большим единицы при какой-нибудь степени пятерки; при этом, для каждого перехода в рамках попытки, четыре числа $d_j$ выбираются псевдослучайно из диапазонов 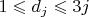$1\leqslant d_j\leqslant3j$
3. Повторяем предыдущий шаг в цикле 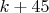$k+45$ раз; если решение еще не найдено, а размер последовательности не увеличился или превысил 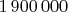$1\,900\,000$ членов - сброс попытки. Если найдено - успех, стоп.

Константы подобраны эмпирически, исходя из физиологии моего нотика и ряда шаманских предположений о пространстве решений задачи. Код (все константы забиты в строках 42, 47, 57, 81):

1. f52isnice(a,b)={return(bitand(real(a),imag(b))==0 && bitand(real(b),imag(a))==0)}; 
2.  
3. f52diff(a,b)={my([L1,R1]=[real(a),imag(a)],[L2,R2]=[real(b),imag(b)],G); 
4. G=bitxor(bitand(L1,L2),bitand(R1,R2)); 
5. return(bitxor(G,bitor(L1,R2))+I*bitxor(G,bitor(L2,R1))) 
6. }; 
7.  
8. f52dec(s,n)={my( 
9. L=binary(real(s)), 
10. R=binary(imag(s)), 
11. L1=select(x->x,L,1), 
12. R1=select(x->x,R,1), 
13. L2=vector(#L1,i,#L-L1[i]), 
14. R2=vector(#R1,i,#R-R1[i]), 
15. r=(sum(i=1,#L2,5^L2[i])-sum(i=1,#R2,5^R2[i]))/(2^n-1); 
16. ); 
17. return([L2;R2;r]); 
18. }; 
19.  
20. f52nb(n)={ 
21. \\try to find a multiple of N=2^n-1 as a sum of b[i]*5^i, i=0,1,...,n-1, b[i]=-1,0,1 
22. t0=getabstime(); 
23. N=2^n-1; 
24. a=vector(n,i,lift(Mod(5^(i-1),N))); 
25. k=floor(vecsum(a)/N); print(k); if(k<2,k=2); 
26. a=vector(n+1,i,if(i<n+1,a[i],N)); \\dunno a nice way for concating two vectors 
27. a=vector(n+2,i,if(i<n+2,a[i],k*N)); 
28.  
29. s=vector(n,i,2^(i-1)); 
30. s=vector(n+2,i,if(i<n+1,s[i],0)); 
31.  
32. \\pack b[i] into bits of a complex number: 5+2i => [101, 10] => 5^2+5^0-5^1 
33. aind=vecsort(a,,1); 
34. a0=vecextract(a,aind); 
35. s0=vecextract(s,aind); 
36. \\print(a); 
37. \\print(s); 
38.  
39. \\DD=7; \\max search depth 
40. \\DD=#combo; 
41.  
42. for(gcnt=1,10000, 
43. print([gcnt,getabstime()-t0,#a]); 
44. a=a0; 
45. s=s0; 
46.  
47. for(ecnt=1,max(30,k+45),\\basically while(1) 
48. wa=#a; 
49. anew=a; 
50. snew=s; 
51. wanew=wa; 
52. waold=wa; 
53.  
54. \\DDgen=random([1,127]); 
55. \\DDgen=binary(DDgen); 
56. \\combo=select(x->x,DDgen,1); 
57. combo=vecsort([random([1,3]),random([1,6]),random([1,9]),random([1,12])],,8); 
58. DD=#combo; 
59.  
60. \\main job 
61. for(dcnt=1,DD, 
62. dep=combo[dcnt]; 
63. da=vector(wa-dep,i,if(f52isnice(s[i+dep],s[i]),a[i+dep]-a[i],-1)); 
64. ds=vector(wa-dep,i,if(f52isnice(s[i+dep],s[i]),f52diff(s[i+dep],s[i]),-1)); 
65. wda=#da; 
66.  
67. anew=vector(wanew+wda,i,if(i<=wanew,anew[i],da[i-wanew])); 
68. snew=vector(wanew+wda,i,if(i<=wanew,snew[i],ds[i-wanew])); 
69. wanew=#anew; 
70. ); \\end for dep 
71.  
72. g=matconcat([anew,snew]~); 
73. aind=vecsort(g,,9); \\remove full duplicates 
74. a=vecextract(anew,aind); 
75. s=vecextract(snew,aind); 
76. if(a[1]==-1,wa=#a;a=a[2..wa];s=s[2..wa]); \\remove one last bad combo s 
77. \\print(["===>",ecnt,#a,combo]); 
78.  
79. if(a[1]==0,print(getabstime()-t0," ms");return(f52dec(s[1],n))); \\success 
80.  
81. if(#a>1900000 || #a==waold, break()); 
82.  
83. ); \\end for ecnt 
84. ); \\end for gcnt 
85. print(getabstime()-t0," ms"); 
86. return([]); \\failure 
87. }; 

Код по-прежнему не экономен к памяти (для размера последовательности $w$ при переходе я пложу несколько объектов размера 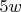$5w$, чтобы иметь возможность пользоваться быстрыми операциями с векторами).