Прямоугольник и квадраты

[Edward_Tur]

Пускай $m$ и $n$ - натуральные числа, причем ни одно из них не кратно шести. Прямоугольник $m\times n$ выложили квадратами $2\times 2$ и $3\times 3$. Доказать, что этот прямоугольник можно выложить квадратами одного вида ($2\times 2$ или $3\times 3$).

[worm2]

В этой задаче я подсмотрел приём, которым эта задача вскрывается (самый красивый приём, который я видел):
Нарисуем наш прямоугольник на системе координат $xOy$ так, чтобы его стороны были параллельны осям, а углы квадратиков $1\times 1$ имели целочисленные координаты. Рассмотрим интегралы:

$$I_{2x}(\Omega)=\iint\limits_\Omega e^{\pi i x}\,dx\,dy$$

$$I_{3x}(\Omega)=\iint\limits_\Omega e^{\frac23\pi i x}\,dx\,dy$$

$$I_{2y}(\Omega)=\iint\limits_\Omega e^{\pi i y}\,dx\,dy$$

$$I_{3y}(\Omega)=\iint\limits_\Omega e^{\frac23\pi i y}\,dx\,dy$$

В качестве областей интегрирования $\Omega$ будем рассматривать прямоугольники с целыми координатами углов. В частности, будем интегрировать по всему прямоугольнику $m\times n$, а также по отдельным квадратам $2\times 2$ и $3\times 3$, которыми он выложен.
Особенности выписанных интегралов таковы:
$I_{2x}(\Omega)=0 \Leftrightarrow$ у прямоугольника $\Omega$ сторона $x$ делится на 2;
$I_{3x}(\Omega)=0 \Leftrightarrow$ у прямоугольника $\Omega$ сторона $x$ делится на 3;
$I_{2y}(\Omega)=0 \Leftrightarrow$ у прямоугольника $\Omega$ сторона $y$ делится на 2;
$I_{3y}(\Omega)=0 \Leftrightarrow$ у прямоугольника $\Omega$ сторона $y$ делится на 3.
Следовательно, на любом квадрате $2\times 2$ и на любом квадрате $3\times 3$ выполняется: $I_{2x}(\Omega)\cdot I_{3y}(\Omega)=I_{3x}(\Omega)\cdot I_{2y}(\Omega)=0$.
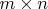
Поскольку наш прямоугольник $m \times n$ выложен из таких квадратов, то и для него: $I_{2x}(m \times n)\cdot I_{3y}(m \times n)=I_{3x}(m \times n)\cdot I_{2y}(m \times n)=0$.
Следовательно, из пары интегралов $I_{2x}(m \times n)$ и $I_{3y}(m \times n)$ хотя бы один равен нулю. Также из пары интегралов $I_{3x}(m \times n)$ и $I_{2y}(m \times n)$ хотя бы один равен нулю.
Что в переводе с языка интегралов обратно (интегралы сделали своё дело и могут уходить) означает, что верны два утверждения:
1) $m$ делится на 2 или $n$ делится на 3;
2) $m$ делится на 3 или $n$ делится на 2.
По условию ни одно из чисел $m$, $n$ не делится на 6. Значит, либо оба числа делятся на 2, либо оба делятся на 3.

[wrest]

У меня получилось собрать два минимальных по площади прямоугольника, выложенного хотя бы одним квадратом 2х2 и хотя бы одним 3х3, со сторонами не кратными 6. Один получился 9х9, второй 8х8
Соотвественно, первый можно наращивать с шагом 3 по каждой стороне (получив например прямоугольник 15х9), а второй с шагом 2 (получив например 10х8). В обоих случаях, обе стороны окажутся или кратными 3 или кратными 2 (т.к. кратные 6 мы вычеркиваем как недопустимые по условиям).
Так что, по крайней мере, похоже на то, что предлагается доказать верное утверждение.

[Edward_Tur]

@worm2 - очень красивый приём!
Решение раскраской:
Рассмотрим сначала случай, когда одно из чисел не делится на два, а другое – не делится на три. Пускай, не ограничивая общности, $m$ - не делится на два, а $n$ - не делится на три.
Раскрасим строки с номерами 1, 3, 4, 6, 7, 9, 10, … прямоугольника $m\times n$ ($m$ - ширина, $n$ - высота). Закрашенных строк у нас нечётное количество, а именное $2\left[\frac{n}3\right]+1$, потому всего закрашенных клеток – нечётное количество. Поскольку каждый квадрат $2\times 2$ и $3\times 3$ покрывает чётное количество закрашенных клеток, то в этом случае выложить прямоугольник квадратами $2\times 2$ и $3\times 3$ невозможно.
У всех других возможных случаях, а именно: $m$ и $n$ одновременно кратны двум или $m$ и $n$ одновременно кратны трём, утверждение задачи очевидно.