Суммарный импульс замкнутой системы.

[K.,bntkm]

rascas в сообщении #1635876 писал(а):

Это допущение неверное. Один шар отдаст пружинам больше двух джоулей, а другой меньше двух джоулей.

Давайте рассуждать логически. Жёсткость пружинок одинаковая. Чтобы вдвинуть пружинки нужны равные силы. Пружинки вдвигаются на равные расстояния. То есть, над обоими пружинками совершаются равные работы по вдвижению бойков. Ну и при выдвижении бойков они будут совершать равные работы при отскоке шаров. Допустим, что мы взяли и остановили шары и они неподвижно висят, соприкасаясь друг с другом. Бойки освобождаются. Шары с равными скоростями отскочат друг от друга. Хотя если пружинки будут разными, то это принципиально никак не влияет на конечный результат. Сначала начнёт сжиматься менее жёсткая пружинка. Как только она сожмётся, начнёт сжиматься более жесткая пружинка. При освобождении бойков сначала распрямиться более жесткая пружинка, а потом менее жесткая. И если шары висят неподвижно, то они отскочат с равными скоростями. Потому как сила действия равна силе противодействия.
Опять же рассуждая логически. Если бы бойки не фиксировались во вдвинутом положении, то произошёл бы обмен скоростями между шарами, так как их массы равны. Но так как пружинки не совершают работу по отталкиванию шаров, то шары отскочат друг от друга с уменьшенными скоростями. Так же допустим, что скорости шаров равны. При ударе бойки фиксируются. Поэтому пружинки не совершают работу при отскоке шаров. Шары отскочат с равными скоростями. Но при этом скорости отскока шаров будут меньше скоростей шаров до столкновения. Суммарный импульс шаров изменится. Но тележка останется неподвижной, так как всё симметрично.

[EUgeneUS]

K.,bntkm в сообщении #1635896 писал(а):

Давайте рассуждать логически.

У Вас не очень хорошо получается рассуждать логически.
Вы находитесь в плену иллюзий и вместо поиска ошибок в своих "логических рассуждениях" пытаетесь навязать свои чудовища, порожденные сном разума, окружающим.
Как указывали выше - так дело не пойдет. Либо Вы начинаете работать над собой: искать у себя ошибки, и слушать других, которые Вам помогают их найти, либо:

DimaM в сообщении #1635797 писал(а):

Если вы продолжите попугаить о чем-то своем, не обращая внимания на ответы, тема вряд ли проживет долго в этом разделе.

-- 10.04.2024, 07:19 --

Запишем баланс энергии (для одинаковых шариков с одинаковыми пружинками):

$\frac{mV_1^2}{2} + \frac{mV_2^2}{2} = \frac{m{V_1'}^2}{2} + \frac{m{V_2'}^2}{2} + U$

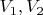
Массу шариков, начальные скорости $V_1, V_2$, и энергию запасенную в пружинке $U$ - считаем известными.
Имеем одно уравнение на два неизвестных. Вы пытаетесь его решить путем "логических рассуждений" - но хоть за рассуждайтесь, если не будет второго уравнения, неопределенность останется.

Второе уравнение нам дает как раз закон сохранения импульса. Но в симметричном случае вместо него можно использовать симметрию. Для этого нужно:
1. Перейти в систему центра масс (скорости в ней буду обозначать буквой $W$).
2. В этой ИСО система совершенно симметрична относительно плоскости удара, так как и шарики одинаковые и пружинки и скорости одинаковы по модулю и противоположны по направлению, то есть тоже симметричны относительно отражения.
3. Из симметрии следует, что и конечные скорости будут симметричны (одинаковы по модулю и противоположны по направлению).
4. И вот тогда можно сделать такое (в ИСО ц.м.):
$\frac{mW_1^2}{2} + \frac{mW_2^2}{2} = \frac{m{W_1'}^2}{2} + \frac{m{W_2'}^2}{2} + U$

Но из симметрии: $mW_1=mW_2$ и $mW_1'=mW_2'$

5. И вот тогда получаем:
$mW_1^2 = m{W_1'}^2 + U$
То есть одно уравнение с одним неизвестным.

6. После чего возвращаемся в лабораторную систему отсчета и находим $V_1, V_2'$.

Проделайте это для Вашей задачи и получите численный ответ.
А до этого - прошу избавить нас от других Ваших "логических" рассуждений.

[K.,bntkm]

EUgeneUS в сообщении #1635898 писал(а):

У Вас не очень хорошо получается рассуждать логически.

Ну хорошо. Объясните, где я ошибаюсь.
1. Шары при столкновении сначала совершают работы по сжатию пружинок.
2. На это затрачивается часть их кинетических энергий.
3. В результате скорость шаров снижается и непосредственно сами шары сталкиваются с меньшими скоростями.
4. Массы шаров равны. Поэтому происходит обмен скоростями между шарами.
5.Поэтому шары и отскакивают с меньшими скоростями, потому что они столкнулись с меньшими скоростями. Ведь энергия в пружинках не участвует в отскоке шаров, так как бойки после вдвижения зафиксировались во вдвинутом положении.
6. А если скорости шаров после отскока стали меньше, то и импульсы шаров стали меньше. Поскольку $P = MV$. То есть, суммарный импульс шаров после столкновения стал меньше, чем до столкновения.
7. Да и закон сохранения энергии как бы соответствует тому, что скорости шаров должны уменьшится. Поскольку часть энергии, запасённой в пружинках, не участвует в процессе отскока шаров.
Я не понимаю, почему так трудно указать на конкретные ошибки в моих рассуждениях?
Ответ написал до прочтения редактирования.

[rascas]

K.,bntkm в сообщении #1635900 писал(а):

3. В результате скорость шаров снижается и непосредственно сами шары сталкиваются с меньшими скоростями.

Да. Но с какими конкретно меньшими скоростями? Это Вы не посчитали.

K.,bntkm в сообщении #1635900 писал(а):

6. А если скорости шаров после отскока стали меньше, то и импульсы шаров стали меньше. Поскольку $P = MV$.

Да.

K.,bntkm в сообщении #1635900 писал(а):

То есть, суммарный импульс шаров после столкновения стал меньше, чем до столкновения.

Уменьшился импульс каждого шара. А вот суммарный импульс шаров не изменился.

[K.,bntkm]

rascas в сообщении #1635901 писал(а):

Уменьшился импульс каждого шара. А вот суммарный импульс шаров не изменился.

Можно подробней объяснить это.

[rascas]

K.,bntkm в сообщении #1635902 писал(а):

rascas в сообщении #1635901 писал(а):

Уменьшился импульс каждого шара. А вот суммарный импульс шаров не изменился.

Можно подробней объяснить это.

Здесь нечего объяснять.
Здесь надо считать. Вам необходимо посчитать суммарный импульс шаров.

Для этого надо найти импульсы каждого шара. И потом сложить эти импульсы векторно.

[sergey zhukov]

K.,bntkm
Импульс - векторная величина. Импульсы складываются векторно. Скажем, два не нулевых вектора могут в сумме дать даже ноль. Или два противоположных вектора могут вырасти или уменьшится на одну и ту же величину, их сумма не изменится. Скалярная энергия так "не умеет".

Прежде чем изобретать инерцоид, неплохо бы изучить сложение векторов. Все же это прямое отношение имеет к инерцоидам. Это займет 10 мин. И ведь вам десять раз про это было сказано. Это и есть самая главная ошибка, которой все повально подвержены: не изучил основы вопроса, а выводы космического масштаба уже готовы. И когда говоришь человеку: изучи основы, он это воспринимает, как будто это вообще не имеет отношения к вопросу. А это и есть ответ на вопрос.

[EUgeneUS]

K.,bntkm в сообщении #1635900 писал(а):

Я не понимаю, почему так трудно указать на конкретные ошибки в моих рассуждениях?

Я не понимаю, почему так трудно следовать указаниям, которые ведут к разбору Ваших затруднений, но легко продолжать рожать чудовищ, рожденных сном разума.

-- 10.04.2024, 08:50 --

rascas в сообщении #1635901 писал(а):

Уменьшился импульс каждого шара

Не факт, вообще говоря. Если в начальный момет шар покоился, то его импульс возрастет (модуль импульса, если быть более точным)

[K.,bntkm]

Чтобы не заморачиваться с пружинками сделаем следующее. Пружинки уберём. А бойки будут входить в шар с трением. Поэтому будем считать, что часть кинетической энергии шаров превращается в тепло. И это тепло уже никак не может участвовать в процессе отскока. И её уже можно не учитывать в расчётах во время отскока шаров.

sergey zhukov в сообщении #1635905 писал(а):

Импульс - векторная величина. Импульсы складываются векторно. Скажем, два не нулевых вектора могут в сумме дать даже ноль. Или два противоположных вектора могут вырасти или уменьшится на одну и ту же величину, их сумма не изменится.

В данном случае вектора не изменяются на одну и ту же величину. Вот если бы шары ударялись и отскакивали с равными скоростями, тогда да. В сумме был бы постоянный 0, так как вектора изменялись бы на равные величины.

-- 10.04.2024, 11:17 --

K.,bntkm в сообщении #1635909 писал(а):

Я не понимаю, почему так трудно следовать указаниям, которые ведут к разбору Ваших затруднений, но легко продолжать рожать чудовищ, рожденных сном разума.

Просто я не силён в математике и наделаю в расчётах много ошибок. Гораздо проще указать ошибки в моих пунктах, где я неправ.

EUgeneUS в сообщении #1635906 писал(а):

Не факт, вообще говоря. Если в начальный момет шар покоился, то его импульс возрастет (модуль импульса, если быть более точным)

Но ведь в нашем случае шары не покоятся.

[sergey zhukov]

K.,bntkm
Ну, я думал, с прошлого раза что-то изменилось. Но нет, ничего не изменилось. Удачи.

[rascas]

K.,bntkm в сообщении #1635909 писал(а):

sergey zhukov в сообщении #1635905 писал(а):

Импульс - векторная величина. Импульсы складываются векторно. Скажем, два не нулевых вектора могут в сумме дать даже ноль. Или два противоположных вектора могут вырасти или уменьшится на одну и ту же величину, их сумма не изменится.

В данном случае вектора не изменяются на одну и ту же величину.

K.,bntkm, вот откуда такое утверждение взялось? Вы посчитайте, и убедитесь, что на одну и ту же величину.

[wrest]

K.,bntkm в сообщении #1635909 писал(а):

Чтобы не заморачиваться с пружинками сделаем следующее. Пружинки уберём. А бойки будут входить в шар с трением.

Я бы предложил ещё более радикальный подход: пусть шары из пластилина, и при соударении слипаются ;)

[K.,bntkm]

Представим цилиндр с 2 шарами внутри, которые находятся у противоположных стенок. Цилиндр закреплён и неподвижен. Шары одновременно отскакивают от стенок цилиндра со скоростями 10 и 20 $m/s$. Кинетические энергии шаров 50 и 200 Дж. Цилиндр освобождён и шары отскакивают с теми же скоростями. В результате цилиндр приходит в движение со скоростью 1 $m/s$. В это время центр масс системы неподвижен. Относительно центра масс скорость шаров 11 и 19 $m/s$. Кинетические энергии шаров в этом случае 60,5 Дж и 180,5 Дж. Кинетическая энергия одного шара увеличилась на 10,5 Дж. Кинетическая энергия другого шара уменьшилась на 19,5 Дж. Энергия не может исчезнуть в никуда. Эта разность энергий в 10 Дж перешла к цилиндру. В результате цилиндр пришёл в движение со скоростью 1 $m/s$. Суммарный импульс шаров одинаков в обоих случаях. Получается, что цилиндр пришёл в движение за счёт только кинетической энергии. А суммарный импульс шаров не изменился. Если цилиндр пришёл в движение со скоростью 1 $m/s$, а получил он 9 Дж, то его масса 18 кг. Я понимаю. что это звучит неправдоподобно - цилиндр пришёл в движения только за счёт приращения кинетической энергии. Хотя суммарный импульс шаров остался неизменным.

[wrest]

K.,bntkm
Вы хотите на кривой козе объехать законы сохранения.
Занятие сомнительное.
Для развеивания непонимания, лучше если вы ясно и точно зададите начальные условия, сделаете рисунок, подпишете что и как.
Ну например, вы пишете:

K.,bntkm в сообщении #1635913 писал(а):

. В это время центр масс системы неподвижен

Но что вы включаете в "систему" не ясно.
Или

K.,bntkm в сообщении #1635913 писал(а):

Представим цилиндр с 2 шарами внутри, которые находятся у противоположных стенок. Цилиндр закреплён и неподвижен. Шары одновременно отскакивают от стенок цилиндра со скоростями 10 и 20 $m/s$.

тоже непонятно -- как-то с середины все началось... Шары сперва находятся у стенок а потом почему-то шары отскакивают - они двигались до этого или что?

[EUgeneUS]

wrest в сообщении #1635928 писал(а):

Вы хотите на кривой козе объехать законы сохранения

Склоняюсь к тому, что это троллинг.
Человек фонтанирует вариантами условий, но ниодну свою задачу решать не собирается.

Как говорят мои знакомые медики в подобных случаях: нас не учили мертвых лечить.