Александр Панчин про магию Вуду

[Ghost_of_past]

EUgeneUS в сообщении #1714143 писал(а):

более правильно говорить, что эти функции ушли от религии в той или иной степени

Разумеется. Но важно тут то, что религия как социальный институт не является больше монополистом по отношению к реализации этих функций.

B3LYP в сообщении #1714144 писал(а):

Вообще, на этом форуме наверно Черниговскую считают эталоном мракобесия

Нет.

B3LYP в сообщении #1714144 писал(а):

между тем она учёный с большими регалиями, любому тут даст фору.

Нет. Вы сейчас какие-то крайности написали.

B3LYP в сообщении #1714144 писал(а):

Именно так была доказана теория эволюции в 19 веке

Нет, не так. И косвенных доказательств существования паранормальных явлений нет, так что в любом случае ничего общего.

[Booker48]

Ghost_of_past в сообщении #1714146 писал(а):

И косвенных доказательств существования паранормальных явлений нет, так что в любом случае ничего общего.

Я бы всё же не согласился. Вернее, это вопрос доверия к источникам.
Я как-то приводил цитаты как достаточно крупных учёных, которые считали Нинель Кулагину мошенницей (часто приводя в качестве доказательства реальный факт её судимости, что некорректно с точки зрения исследования её феномена), так и цитаты учёных, уверенных в том, что некий феномен таки существовал. Некоторые из исследователей занимали промежуточную позицию, полагая, что явления ею не фальсифицировались, но могли быть объяснены с физиологической точки зрения. При этом признавали, что механизм этих физиологических проявлений не установлен.

[Ghost_of_past]

Booker48 в сообщении #1714147 писал(а):

Я бы всё же не согласился.

Простите, но здесь никакого несогласия быть не может: иное как раз лженаука в чистом виде.

Booker48 в сообщении #1714147 писал(а):

так и цитаты учёных, уверенных в том, что некий феномен таки существовал

Это не косвенное доказательство. То, что кто-то что-то считает истинным - это вообще не доказательство. По крайней мере в эмпирических науках. Вот в юриспруденции в определенных ситуация это может быть косвенным доказательством, например в судебном процессе, в абстрактных науках - тоже, а в эмпирических науках - нет.

[realeugene]

По ссылке выше:

Цитата:

Но самое смешное было в следующем: фокусники договорились, что если их хоть раз спросят, как они это делают, то они честно признаются. И за несколько лет исследований никто не задал им этот вопрос. Зато про одного из фокусников успели написать диссертацию.

-- 06.01.2026, 20:18 --

B3LYP в сообщении #1714144 писал(а):

Я давно исхожу из "принципа суммирования аргументов": если есть множество средних аргументов в пользу какого-то тезиса, то в сумме они превращаются в доказательство.

Чушь. Если есть тыща ложный высказываний, они все вместе ложные, как их ни суммируй.

[B3LYP]

realeugene в сообщении #1714154 писал(а):

Чушь. Если есть тыща ложный высказываний, они все вместе ложные, как их ни суммируй.

Хорошо, процитирую сам себя:

Здесь появляется очень важный момент: большое количество слабых аргументов могут в сумме превратиться в сильный аргумент.

В теории вероятностей это называется “теорема сложения произвольных событий”. Её можно проиллюстрировать следующими аналогиями:

1) Предположим, произошло убийство и у суда есть подозреваемый. Один из свидетелей заявляет, что он видел как подозреваемый совершил преступление. Это заявление, скорее всего, сочтут недостаточно достоверным для доказательства вины обвиняемого. Но если много разных людей заявляют одно и то же – что они видели этого обвиняемого на месте преступления – суд может счесть это доказательством. При этом важно, однако, исключить возможность сговора между этими свидетелями;

2) Если вы играете с кем-то в азартную игру на деньги, и обнаруживаете что систематически проигрываете - это может говорить о мошенничестве со стороны оппонента. Когда игр сыграно немного, средний проигрыш является только слабым аргументом в пользу гипотезы о мошенничестве, но чем больше партий сыграно и чем больше суммарный средний проигрыш - тем вероятнее становится правомерность этой гипотезы;

3) В химии при структурной идентификации веществ по спектрам совпадения отдельных полос образца и эталона могут быть слабыми аргументами, но чем этих совпавших полос больше, тем увереннее становится идентификация;

4) При идентификации человека по биометрическим данным, отдельные совпадения, опять же, могут быть слабыми аргументами, но когда совпадений много, это превращается в доказательство.

Для аналогии с судом теорему сложения произвольных событий можно проиллюстрировать на конкретным примерах. Предположим, свидетель A заявляет, что он видел как подозреваемый совершает преступление; мы знаем, что он говорит правду с вероятностью 90%, соответственно с вероятностью 10% он лжёт. Если свидетель B заявляет то же самое, он также говорит правду с вероятностью 90%. Если они оба заявляют одно и то же, то вероятность того, что они оба лгут, становится равной произведению вероятностей, что лжёт каждый из них. Т.е. мы получаем эту вероятность равной $0.1 \cdot 0.1=0.01$. 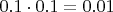Таким образом, вероятность того, что они сказали правду, становится равной 99% - это уже намного ближе к доказательству (уточнение: в данном случае перемножаются именно вероятности лжесвидетельств, поскольку нечестный человек может сказать правду, в то время как честный не может сказать неправду). 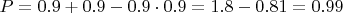В криминалистике обычно используется формула "вероятность суммы двух произвольных событий равна разности суммы и произведения вероятностей этих событий", которая даёт тот же результат: в данном случае $P=0.9+0.9-0.9 \cdot 0.9=1.8-0.81=0.99$.

[realeugene]

B3LYP в сообщении #1714156 писал(а):

Предположим, свидетель A заявляет, что он видел как подозреваемый совершает преступление; мы знаем, что он говорит правду с вероятностью 90%

Если начинаете рассуждать про вероятности - определите сначала пространство событий, иначе это всё бла-бла, а не теорвер. И потом вдруг окажется, что пространства событий у вас нет, и, следовательно, перемножать вероятности вы просто не можете.

[B3LYP]

realeugene

Я не хочу вам отвечать, считайте что я слил дискуссию.

[mihaild]

B3LYP в сообщении #1714156 писал(а):

В криминалистике обычно используется формула "вероятность суммы двух произвольных событий равна разности суммы и произведения вероятностей этих событий"

Ага, а объем кита примерно равен $\pi R^2 l$, где $\pi$ - константа, которая для гренландских китов примерно равна трём.

B3LYP в сообщении #1714156 писал(а):

Здесь появляется очень важный момент: большое количество слабых аргументов могут в сумме превратиться в сильный аргумент

Ага, Вы первый человек в мире, узнавший о тервере и статистике. Джейнс у Вас свою книгу украл. Хотя на таком уровне, скорее всего, правила рассуждений понимали еще древние греки.
Человечеством накоплено довольно много свидетельств и за, и против паранормальщины. И аггрегировав их, можно с очень большой степенью уверенности утверждать: не бывает. Подробнее смотри того же Панчина, или что-то чуть менее детское, вроде "Псевдонаука и паранормальные явления".

[Ghost_of_past]

B3LYP в сообщении #1714156 писал(а):

Здесь появляется очень важный момент: большое количество слабых аргументов могут в сумме превратиться в сильный аргумент.

Вот только Вы не привели ни единого такого слабого аргумента, который можно было бы засчитать за эмпирическое обоснование существования паранормального.

B3LYP в сообщении #1714156 писал(а):

Но если много разных людей заявляют одно и то же – что они видели этого обвиняемого на месте преступления – суд может счесть это доказательством

Суд обязан учесть любые показания, единственные или множественные, как доказательства - конечно, если эти показания отвечают необходимым критериям уголовно-процессуального законодательства для доказательств. Вопрос отнюдь не в этом, а в том, что в апелляции решение может развалиться при условии, что были другие доказательства, а суд их толком в решении не учел или же если были допущены грубы процессуальные и доказательные ошибки, например достаточно процессуально неправильно оформить доказательства или, к примеру, выбить информацию из подозреваемого незаконным способом и тогда даже если подозреваемый сам условно покажет закопанный труп, то в суде это доказательство и все косвенные доказательства (экспертиза трупа и т.д.) уже не смогут применяться (это доктрина fraus omnia corrumpit, известная еще с римского права).

B3LYP в сообщении #1714156 писал(а):

В криминалистике обычно используется формула "вероятность суммы двух произвольных событий равна разности суммы и произведения вероятностей этих событий"

В криминалистике это формула обычно как раз не используется для свидетельских показаний, т.к. она используется для несовместных событий, а свидетельские показания таковыми обычно не считаются. Она используется при более строгих видах анализа - например, анализе ДНК или отпечатков пальцев.

[Mikhail_K]

Ghost_of_past в сообщении #1714162 писал(а):

В криминалистике это формула обычно как раз не используется для свидетельских показаний, т.к. она используется для несовместных событий

Уточнение: не для несовместных, а для независимых событий $P(A\cup B)=P(A)+P(B)-P(A)P(B)$.

[realeugene]

Ghost_of_past в сообщении #1714162 писал(а):

Вот только Вы не привели ни единого такого слабого аргумента, который можно было бы засчитать за эмпирическое обоснование существования паранормального.

Миллионы детей уверены в существовании Санта Клауса.

[Anton_Peplov]

Mikhail_K в сообщении #1714163 писал(а):

Ghost_of_past в сообщении #1714162 писал(а):

В криминалистике это формула обычно как раз не используется для свидетельских показаний, т.к. она используется для несовместных событий

Уточнение: не для несовместных, а для независимых событий $P(A\cup B)=P(A)+P(B)-P(A)P(B)$.

Эта формула верна для произвольных событий, в этом ТС прав.

[warlock66613]

Anton_Peplov в сообщении #1714173 писал(а):

Эта формула верна для произвольных событий

Эта -- нет. $P(A\cup B)=P(A)+P(B)-P(A \cap B)$ -- да.

[B3LYP]

(Оффтоп)

Ghost_of_past в сообщении #1714162 писал(а):

Вот только Вы не привели ни единого такого слабого аргумента, который можно было бы засчитать за эмпирическое обоснование существования паранормального.

Аргументов много, в последнее время и достаточно сильных - например сейчас есть много сбывшихся и частично сбывшихся пророчеств. Я не буду тут это выкладывать, чтобы не нарываться.
Вот ещё отмечу в тему. Я считаю, что широкий кругозор даёт достаточно хорошую защиту от шизофрении, это самый эффективный метод лечения шизофрении. Мне этот форум нравится тем, что здесь есть как физический раздел, так и биологический, экономический, плюс Свободный полёт и Междисциплинарный раздел, где можно всё это смешивать. Но у меня есть и много других интересов, сфер которые я изучаю от избытка свободного времени - а то что я узнаю в этих сферах, тоже влияет на мировоззрение, и суммарно всё, что я знаю из разных областей науки и "лженауки", сливается в единую достаточно целостную логически картину мира. Поэтому я считаю себя более разумным, чем остальные участники этого форума. Сорри что так тупо хвалю себя.

[Red_Herring]

(народная примета)

Есть поверье, что как проведешь период между новым Новым Годом и старым Новым Годом, так и до конца года будет. Если это справедливо, то многим высокоученым и глубокоуважаемы участникам форума придется носить воду решетом и спорить с альтернативными гениями.