Understanding this definition of measure function.

[Combat Zone]

Knight2023 в сообщении #1622114 писал(а):

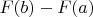
As $\delta$ can be made as small as we please, we have the infimum $F(b) - F(a)$ and it well corresponds with the notion of length of an interval.

Верно, $\mu_F([a,b])=F(b)-F(a)$ в силу непрерывности $F$.
В качестве покрытий в данном случае достаточно было выбирать систему полуинтервалов $(a-\delta,b]\supset [a,b]$, где $\delta>0$ произвольно.
Это способствует интуитивному пониманию, чему будет равна мера. Но строго говоря, отсюда следует, что $\mu_F([a,b]\le F(b)-F(a)$. Поскольку мера - инфимум по покрытиям "почти" произвольного вида. А инфимум по более широкому набору покрытий будет не превосходить инфимума по более узкому - тому, который мы выбрали.

Так что с равенством, если хочется, можно еще повозиться, а можно и уже и нет, если нужный уровень понимания достигнут.

[Knight2023]

Combat Zone
I guess, yes, I have reached an understanding. Thank you for being with me.

Thank you everyone.