Здравствуйте! Возник вопрос по использованию функции WhenEvent для решения задачи оптимального управления, где есть переключения.
Ниже я приведу ту систему, которая рассматривается. Управление
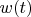
меняется в зависимости от знака функции

по формуле . Я решил реализовать интегрирование системы с некоторыми начальными условиями

,

,

,

,





,

.
Однако у меня переключение управления происходит не в момент смены знака

, а в какой то другой. И еще переключается, когда

Код:
SolveDE[DiffEq_, T_, initCond_, CinematicEq_, condCinematic_] :=
NDSolve[DiffEq~Join~CinematicEq~Join~condCinematic~Join~initCond~
Join~{WhenEvent[
Subscript[\[Psi], \[Beta]][t]/
r[t] (b Sin[\[Beta][t]] -
Sin[-ArcTan[
Subscript[\[Psi], \[Beta]][t]/Subscript[\[Psi], r][t]*
w[t]/r[t]]]) > 0, {w[t] -> w2}],
WhenEvent[
Subscript[\[Psi], \[Beta]][t]/
r[t] (b Sin[\[Beta][t]] -
Sin[-ArcTan[
Subscript[\[Psi], \[Beta]][t]/Subscript[\[Psi], r][t]*
w[t]/r[t]]]) < 0 , {w[t] -> w1}]}, {r[t], \[Beta][t],
Subscript[\[Psi], r][t], Subscript[\[Psi], \[Beta]][t], w[t],
Subscript[x, P][t], Subscript[x, \[CapitalEpsilon]][t],
Subscript[y, P][t],
Subscript[y, \[CapitalEpsilon]][t], \[Theta][t]}, {t, T},
DiscreteVariables -> {w[t] \[Element] Reals},
StartingStepSize -> 0.1,
Method -> {"FixedStep", Method -> "ExplicitRungeKutta"},
StepMonitor :>
Print["t = ", t, " r(t)=", r[t], " \[Beta](t)=", \[Beta][t],
" \!\(\*SubscriptBox[\(\[Psi]\), \(r\)]\)(t)=",
Subscript[\[Psi], r][t],
" \!\(\*SubscriptBox[\(\[Psi]\), \(\[Beta]\)]\)(t)=",
Subscript[\[Psi], \[Beta]][t], " \[Alpha](t)=", \[Alpha][t],
" w(t)=", w[t], " \!\(\*SubscriptBox[\(H\), \(1\)]\)(t)= ",
Subscript[H, 1][t]]];
Хотел задать вопрос о том, как все таки работает функция WhenEvent и как ее эффективно использовать для решения дифф. уравнений с переключением?
Я вижу себе это так: при

по заданным начальным условиям у меня известно значение

исходя из знака

. Начинаю интегрировать с

, которое выбирается по правилу и на следующих временах и проверяю условие: если

, то я в этот момент времени сменяю
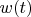
на другое и так далее. Если вдруг

, то сменяю снова. Т.е. переключение происходит при переходе функции

через ноль. Однако в таблице как можно видеть, переключение происходит в момент, когда

знакопостоянна..
Может я неправильно логику понимаю этой функции?