Приоритет операций в логике нулевого порядка / высказываний

[dadbdcdd]

Есть ли канонически определенный порядок операций в логике нулевого порядка / логике высказываний / булевых алгебрах?
Достаточно простой вопрос, но как оказалось, я использую информацию ничем не потвержденную и хочу разобраться.

Я привык использовать приоритеты, как описано в этой таблице:


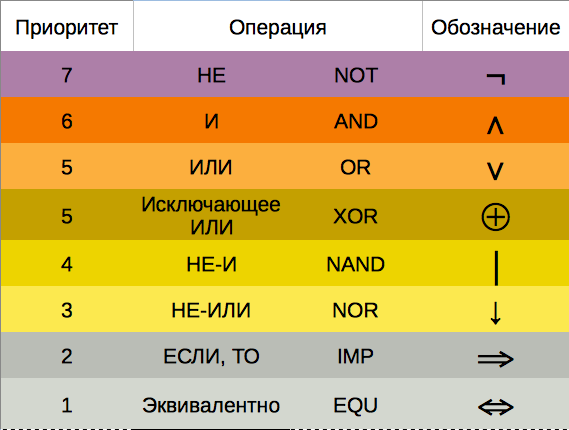
Такой порядок был определен в книге Дискретная Математика Андерсона.

Но, предположим, есть выражение a⊕b∨c
В каком порядке выполнять операции?
Если воспринимать формулу как (a⊕b)∨c, то вектор ее значений будет 01111101.
Если воспринимать формулу как a⊕(b∨c), то вектор ее значений будет 01111000.

Если по Андерсону и таблице выше, то ответ был бы a⊕(b∨c) = 01111000.
Если пользоваться некоторыми другими источниками и калькулятором (https://programforyou.ru/calculators/po ... -sknf-sdnf), то результат был бы 01111101.

Есть ли какой-то стандарт? Ну или достаточно серьезная литература на которую можно ссылаться?

Ибо выражения без скобок встречаются часто, в различных учебниках, практикумах.
А порядок выполнения определяется по разному.
Особенно интересует ситуация с суммой по модулю 2, штрихом шеффера и стрелкой пирса.

Отрицание, коньюнкция, дизьюнкция, импликация и еквиваленция практически везде описаны, что следуют в написанном тут порядке.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.