Профиль вибрационной нагрузки в Environmental Testing

[Schwungrad]

Постановка задачи: рассмотреть возможность уменьшения амплитуд профиля инерционной нагрузки при тестировании ротора электромотора.

Инерционная нагрузка для тестирования электромотора в осевом (направлении оси ротора) направлении задана в виде таблицы ($\Omega$ - частота возбуждения, $A_1$ - амплитуда ускорения):

\begin{table}[] \begin{tabular}{|c|c|} \hline Frequency \Omega {[}Hz{]} & Acc. Amplitude RMS A_1 {[}\frac{m}{s^2}{]}\\ \hline 20 & 1.5 \\ \hline 50 & 1.5 \\ \hline 60 & 0.8 \\ \hline \ldots & \ldots \\ \hline 1880 & 3.7 \\ \hline 2000 & 3.7 \\ \hline \end{tabular} \end{table}

Данная инерционная нагрузка определена для Environmental Testing электромотора, который жестко крепится к скользящему столу шейкера с помощью специального массивного адаптера (fixture).
Профиль ускорения прилагается к адаптеру, таким образом, что в одной или нескольких контрольных точках измеряется ускорение и реализуется контроль его амплитуды (используется допустимых коридор между верхним и нижним допустимым значением амплитуды). Скорость изменения частоты возбуждения - 1/3 октавы в минуту. После прогонки частоты возбуждения от минимального до максимального значения, происходит симметричное уменьшение частоты в обратном направлении. Медленно вращаясь, т.к. без вращения образуются раковины в подшипниках, мотор тестируется, таким образом, 24 часа.

Пример испытуемого электромотора (DUT):



Пример скользящего стола шейкера с закрепленным с помощью адаптера электромотором:



Вопрос: можно ли из физических соображений уменьшить инерционную нагрузку, если требуется тестировать не мотор целиком, а только ротор мотора?

Из уравнений простейшей одномассовой модели следует, что нельзя. Но прав ли я на самом деле, ведь не были учтены потери энергии при соударениях в подшипниках и демпфирование?

Ход рассуждений. Предполагаем, что можно использовать двухмассовую модель (масса - пружина) и что инерционная нагрузка идеально распределена в статоре. Тогда:



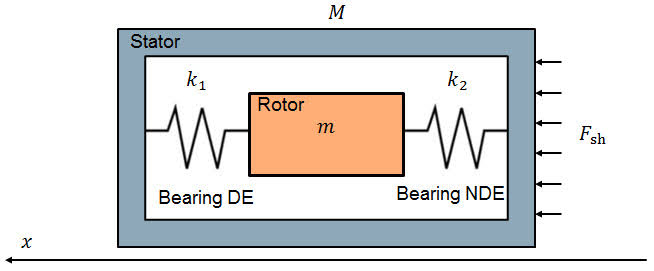
Уравнения движения:

$$ \begin{cases} M\ddot x_{1}+k_1\bigl(x_1 - x_2\bigr) + k_2\bigl(x_1 - x_2\bigr)=F_{\rm s h} \\ m\ddot x_{2} - k_1\bigl(x_1 - x_2\bigr) - k_2\bigl(x_1 - x_2\bigr)=0 \end{cases} $$

Здесь $M,\ m$ - масса статора и ротора, $k_1,\ k_2$ - жесткость подшипников в направлении оси мотора, $x_1,\ x_2$ - перемещение статора и ротора.

Условие идеального распределения инерционной нагрузки в статоре:

$$ \ddot x_{1}=A_1\cos(\nu t) \quad \Rightarrow \quad x_{1}=-\frac{A_1} {\nu^2} \cos(\nu t) $$

Откуда получаем:

$$ m\ddot x_{2} + \bigl(k_1 + k_2\bigr)x_2 = \bigl(k_1 + k_2\bigr)x_1 = -\frac{A_1} {\nu^2}\bigl(k_1 + k_2\bigr) \cos(\nu t) $$

или, обозначив $\omega$, $f$ собственную частоту и амплитуду возбуждения:

$$\ddot x_{2} +\omega^2 x_2 = -f \cos (\nu t), \quad \textsf{где} \quad \omega^2 = \frac{k_1 + k_2} {m}, \quad f=A_1 {\Bigl(\frac{\omega}{\nu}\Bigr)}^2$$

Частное (установившееся) решение последнего уравнения:

$$x_{2} = -\frac{1}{\omega^2 - \nu^2} f \cos (\nu t)$$

и следовательно:

$$\ddot x_{2} = \frac{\nu^2}{\omega^2 - \nu^2} f \cos (\nu t)= \frac{\omega^2}{\omega^2 - \nu^2} A_1 \cos (\nu t)$$

или

$$\ddot x_{2} = A_2 \cos (\nu t), \quad \textsf{где} \quad A_2=\frac{\omega^2}{\omega^2 - \nu^2} A_1 $$

И, следовательно, если пренебречь потерями энергии, то $A_2>A_1$. То есть, получается, что профиль амплитуды инерционной нагрузки ротора уменьшить нельзя.

[Pphantom]

Тема перемещена из форума «Механика и Техника» в форум «Карантин»
по следующим причинам:

- не набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- табличные данные в таком виде также почти совершенно бесполезны, если они важны, их надо вставить в виде текста.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Механика и Техника»