Метод простой итерации при решение системы нелинейных уравне

[corbulo]

Здравствуйте, помогите разобраться.
Есть система:
\left\{\!\begin{aligned} & \operatorname{ctg}{(x1 * x2 + 1)} = 4x1^2 \\ & 2x1^2+4x2^2=60 \end{aligned}\right.
Привел ее к следующему виду:
\left\{\!\begin{aligned} & x2 = \frac{ \operatorname{arctg}(\frac{ 1 }{ 4x1^2 } )-1 }{ x1 } \\ & x1 = \pm \sqrt{30 - 2 * x2^2} \end{aligned}\right.
Нашел только один корень: \begin{pmatrix} 5.471224542968644\\-0.18125480190310334 \end{pmatrix}
Matlab мне находит 8 корней. Как найти остальные?
Потом привел систему к следующему виду:
\left\{\!\begin{aligned} & x1 = \frac{ \operatorname{arctg}(\frac{ 1 }{ 4 * x1^2 } ) - 1 }{ x2 } \\ & x2 = \pm \sqrt{15 - 0.5 * x1^2} \end{aligned}\right.
Начальное приближение взял:
x1 = -1.02
x2 = 3.80

Проверил условие сходимости:
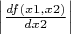
\left| \frac{ df(x1,x2) }{ dx1 } \right| + \left| \frac{ df(x1,x2) }{ dx2 } \right|< 1 тоже самое для второй функции, но почему-то корень выдает x1 = 0.12999257113101675, x2 = 3.8718925969338316. Корень у меня такой есть, но мне нужен другой, то есть x1 \approx -1.02757 x2 \approx 3.80421

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу math» и видеоролик Как записывать формулы): нижние индексы набираются как $x_1$, звездочку не надо использовать как знак умножения (надо либо ничего, либо $a \cdot b$, либо $a \times b$), отдельные выражения вроде $x \approx 5$ надо набирать целиком, а не только центральную часть.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.