"Симметричность" тензоров

[Hagrael]

Доброго времени суток, уважаемые математики! Сейчас читаю про тензоры в книге "Основы векторного исчисления" (Дубнов), изучаю основные свойства тензоров.

Тензоры, как и любые другие дифференциально-геометрические объекты, можно преобразовать так, что их компоненты будут зависеть от других координат, то есть их можно привести к другой параметризации. 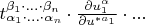Это можно сделать по следующей формуле (индексы при u без звёздочки представляют собой индексы сум по Эйнштейну - суммы произведений вида $A_\alpha B_\alpha$; учитывая количество пар таких индексов, можно сказать, что на самом деле здесь идёт сумма вида $t^{\beta_1\cdot...\cdot\beta_n}_{\alpha_1\cdot...\cdot\alpha_n}\cdot\frac{\partial u^\alpha_1}{\partial u^{* a_1}}\cdot...$ - $a$ в знаменателе является латинскаой, а не греческой):

(формула 1)

И этот процесс затем можно применить к свежеполученному (полученному из тензора $А$) тензору $B$ и получить тензор $C$. И суть в том, что такое поэтапное что при переходе от параметризации тензора $A$ к параметризации тензора $С$ можно осуществить за раз, если известны соответствующие производные для мгновенного перехода (производные координат тензора $А$ по $С$).

Это и называется "симметричностью" тензоров. И в книге доказательство "симметричности" тензоров осуществляется следующим образом:


(Доказательство "симметричности"

И ключевым моментом является перемножение производных в слагаемых по Эйнштейну:

(формула 2)

В этой ключевой формуле 2 индексы $\alpha_1$ и $c_1$ являются индексами по Эйнштейну. Утверждается, что такое произведение равняется "символу Кронекера", взятому по этим же индексам. Данный "символ Кронекера" равняется $1$, если коэффициенты совпадают и $0$, если не совпадают. Но разве это так? Ведь если $\alpha_1\ne c_1$, то это произведение не будет равно $0$! Ведь в этом случае первая производная может быть не равна $0$, и вторая - тоже (довод 1)! Я понимаю, что хочется сократить $\partial a_1$ и тогда получится, что мы придем к производной одной координаты по другой, которая равна $0$ (только потому что обе координаты принадлежат одной и той же параметризации!), но ведь довод 1 все ещё имеет смысл! Почему же он не должен быть верен Возможно, что довод 1 имеет место быть и соответствующие произведения производных раны $0$, но при этом сумма нескольких таких слагаемых при $\alpha_1\ne c_1$ равна $0$? Скорее всего, так, но почему, я пока-что не понимаю.

Уважаемые математики, хотел бы в этом разобраться и прошу вашей помощи!

[пианист]

Hagrael в сообщении #1539311 писал(а):

Но разве это так?

Это именно так.
$f \circ f^{-1} = id$, а матрица Якоби от $id$ есть единичная матрица

[svv]

Hagrael в сообщении #1539311 писал(а):

Возможно, что довод 1 имеет место быть и соответствующие произведения производных не раны $0$, но при этом сумма нескольких таких слагаемых при $\alpha_1\ne c_1$ равна $0$?

Да, так и есть. Там же ещё суммирование по индексу $a_1$. Если какое-то слагаемое в сумме ненулевое, обязательно найдутся противоположные ему по знаку.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- не набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы), тем более что фактически для понимания смысла вопроса достаточно набрать "формулу 2", которая к тому же на скане видна крайне плохо.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.