Уважаемые участники форума, кто то можно указать источники(материалы) на исследование функции типа :

, где

?
Мне интерисует поведение этоя функция когда :
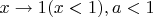
;

;

;

;

;
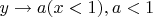
;

;

;

;

;

;

;
А также поведение когда:

;

;

;

;

;

;

;

;
Подозреваю, что в этих точек есть какие то экстремумы.
Интересно какая поверхность получается при изменения

в зависимости от то

.
Хорошо будет посмотреть, если есть она(или её части) вычертаная(ые) с какиим то ППП.