Вы сравнили друг с другом, всё сошлось, но назвали величины неправильно, это не максимум

, а ровно

. Ошибся venco, Вы с ним согласились, не поправили.
Ну что же, сутки прошли, уважаемый
venco промолчал. Тогда я скажу.
А я вот не считал и не считаю, что
venco здесь ошибся. Потому и не поправил. Обратите внимание,
речь о максимумах идёт с самого первого поста. Я уже выделял болдом, сделаю это и сейчас.
Количество строк разной длины с разной максимальной длиной повторений начинается так:

Да, о
максимумах здесь речь снова идёт. Это наш знаменитый треугольник, то бишь удвоенные элементы матрицы

в программе.
Как мы его формируем? Допустим, вручную. Я в своё время вручную дошёл как раз до

-й строчки и только тогда заглянул в OEIS.
Кодируем последовательности бросков двоичными числами и для определённого количества бросков перебираем их все подряд по некоему алгоритму, чтобы ничего не пропустить и, наоборот, не посчитать более одного раза. Затем сортируем, например, приплюсовывая

к тому или иному столбцу.
Вот встретилась у нас такая серия из

-ми бросков:

Какой столбец нам наращивать на

? У нас здесь есть и

, и

, и

, и

, и

, и

. Да, подстрока из трёх нулей подряд тоже есть. Ответ: по подстроке
максимальной длины, то есть

, то есть наращиваем

-й столбец. Всего таких серий(из

бросков с
максимальной длиной

) —

.
То есть для формирования треугольника,
максимумы нам необходимы. Не обязательно при этом складывать те или иные его элементы между собой. Случаи, когда это нужно делать, лучше оговаривать отдельно. А именно про сумму сказано не было:
Для

вероятности получить
максимальный повтор

равны:
То есть надо использовать элементы первых

-ти столбцов
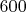
-й строки. Но не складывать их.
Да уже ничего, все разногласия в цифрах устранены,
Вот здесь
mihaild был не согласен:
Где-то лишняя двойка, должно быть в два раза меньше (в варианте, когда мы требуем чтобы ни нуль ни единица не повторялись больше 6 раз).

 , а ровно
, а ровно 
 в программе.
в программе. -й строчки и только тогда заглянул в OEIS.
-й строчки и только тогда заглянул в OEIS. к тому или иному столбцу.
к тому или иному столбцу.
 , и
, и  , и
, и  , и
, и  , и
, и  . Да, подстрока из трёх нулей подряд тоже есть. Ответ: по подстроке
. Да, подстрока из трёх нулей подряд тоже есть. Ответ: по подстроке  , то есть наращиваем
, то есть наращиваем  .
. вероятности получить
вероятности получить  равны:
равны: -ти столбцов
-ти столбцов 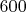 -й строки. Но не складывать их.
-й строки. Но не складывать их. бросках появится отрезок одинаковых букв длины
бросках появится отрезок одинаковых букв длины  (в тексте
(в тексте  ). Но что-то достаточно простого решения не просматривается (может, просто устала к концу недели
). Но что-то достаточно простого решения не просматривается (может, просто устала к концу недели ![$T[]$ $T[]$](https://dxdy-03.korotkov.co.uk/f/2/a/7/2a745078d5904b2b0d9499f865acfd7b82.png) конечно же случаи когда максимальная длина ровно
конечно же случаи когда максимальная длина ровно  вообще, для ответа на него и надо просуммировать вероятности
вообще, для ответа на него и надо просуммировать вероятности  . А для ответа на вопрос "какова вероятность выпадения не длиннее
. А для ответа на вопрос "какова вероятность выпадения не длиннее  — вот это я и считал "получить максимальный повтор
— вот это я и считал "получить максимальный повтор 







 на исходный вектор.
на исходный вектор. имел 1 в первом элементе и нули в остальных.
имел 1 в первом элементе и нули в остальных. .
. даёт вероятность того, что где-то встретилась последовательность минимум из 6 орлов.
даёт вероятность того, что где-то встретилась последовательность минимум из 6 орлов. .
. , то студент халявничал.
, то студент халявничал.



 знаков.
знаков.