Отрезки из повторяющихся исходов

[Yadryara]

provincialka в сообщении #1532012 писал(а):

$$\begin{matrix} 1& 2 & 3 & 4 & 5 & 6 \\ 31441& 374866 & 343248 & 156832 & 62197 & 31416 \end{matrix}$$

Для первого и последнего чисел точное значение $1000000\cdot 2^{-5}=31250$, так как в этих случаях состав последовательности вполне определяется первой выпавшей буквой.

Конечно. Значит, ни у меня, ни у Вас для 6-ти бросков ошибки нет. Матожидания:

$$\begin{matrix} 1& 2 & 3 & 4 & 5 & 6 \\ 31250& 375000 & 343750 & 156250 & 62500 & 31250 \end{matrix}$$

[mihaild]

venco в сообщении #1532014 писал(а):

уже для 10000 бросков вероятность получить максимум 6 повторов $1.66722\cdot10^{-36}$

Где-то лишняя двойка, должно быть в два раза меньше (в варианте, когда мы требуем чтобы ни нуль ни единица не повторялись больше 6 раз).

(точное значение)

16630839093886493318310206208188770135256932429697303508167572537892964490039810715739361410004224654319481067279590832171408485303141421420892126780495269036609028984281135905443030145695727065427793524431023062354495358754347494992636385416444367188556731610943177417016551507278045737629888991190599963035873845566689771383516911822609650593260212095818581983576648438707306960900589152565606100975675363922447378694205850060836688412254084677083635006612124532259202724247038629570907108111112711060533959001108985186506640756356127401710731353717109019758771780803972330352326400329351586487828503612636631505676111650917991958456512752101032151511783372866008708205347828627191994064748228530505452890836286883795170156174721262893960362788411772729946597504234967442266175150921379567699712311153014868787033261371551434091851272771956360840530459739654304489663144129947683224331367257471131219180444091957729274659072291019327135619687161466523529523323434461008223870871515097771105635688244181769374294352781853561418666765843419670271598052619327377549927214529421195199588975297168279007232092301523408247963981623511802531370377300757971284567455524332980543542768148901835359277917542913191931513862006133299681362511814317325368462060239395200995944657569636935435272868894040306141513949756345267195441472089683928625587724846167621815908912793642010615868351589703943960879021966270329356771857168759434914424756407003328464390326897693095884894777882653866133324444137345218913285000704256106067177824124684745355654878932532407265602981870348981800719845324317575710922726719722612288622660679515904981660163320022291123314722623326423423309514707771334341817220045097051646882410238020122645513136906489173508040229103593103241969338561665505028813627451971161996595607985073911148194560940337739799559292094638247850504427367485608025599564609433990112481961939432240273161627181225567311262452872951921281479984905110764088310695012812853740050106045154659239080174474486895733857574231745047843440483014894832174146763114219735906809360555115143662512499703442730690119490367112422716761484021002605986658855830395875288556932029325847835793255904528416484271629170840148636773666378780356818537659572461613065365118946227192059120296322629119573026306933943227211890099354874142305156619442414771723778949466441193311439871971850959162165437525734014638577720044375401222910301107519630266461407773955361004785202171577606383040749888126917035093654465463668056410591553876230441760568544669510769390119267680139870047510396810794266563580000296881044903798826487369500549195777376473684491405902096264694236572299707735581848081925979763030053204968973173346161009102893107172245580492823875218732389702334905128573587877941224479045403788389447517978107057930197882089635666804907725067905734459593884018142296030839873223151853655774229552938891442346336301390734004488600957911570173781524150980826756450117247790146084492575041839979426080046280 / 19950631168807583848837421626835850838234968318861924548520089498529438830221946631919961684036194597899331129423209124271556491349413781117593785932096323957855730046793794526765246551266059895520550086918193311542508608460618104685509074866089624888090489894838009253941633257850621568309473902556912388065225096643874441046759871626985453222868538161694315775629640762836880760732228535091641476183956381458969463899410840960536267821064621427333394036525565649530603142680234969400335934316651459297773279665775606172582031407994198179607378245683762280037302885487251900834464581454650557929601414833921615734588139257095379769119277800826957735674444123062018757836325502728323789270710373802866393031428133241401624195671690574061419654342324638801248856147305207431992259611796250130992860241708340807605932320161268492288496255841312844061536738951487114256315111089745514203313820202931640957596464756010405845841566072044962867016515061920631004186422275908670900574606417856951911456055068251250406007519842261898059237118054444788072906395242548339221982707404473162376760846613033778706039803413197133493654622700563169937455508241780972810983291314403571877524768509857276937926433221599399876886660808368837838027643282775172273657572744784112294389733810861607423253291974813120197604178281965697475898164531258434135959862784130128185406283476649088690521047580882615823961985770122407044330583075869039319604603404973156583208672105913300903752823415539745394397715257455290510212310947321610753474825740775273986348298498340756937955646638621874569499279016572103701364433135817214311791398222983845847334440270964182851005072927748364550578634501100852987812389473928699540834346158807043959118985815145779177143619698728131459483783202081474982171858011389071228250905826817436220577475921417653715687725614904582904992461028630081535583308130101987675856234343538955409175623400844887526162643568648833519463720377293240094456246923254350400678027273837755376406726898636241037491410966718557050759098100246789880178271925953381282421954028302759408448955014676668389697996886241636313376393903373455801407636741877711055384225739499110186468219696581651485130494222369947714763069155468217682876200362777257723781365331611196811280792669481887201298643660768551639860534602297871557517947385246369446923087894265948217008051120322365496288169035739121368338393591756418733850510970271613915439590991598154654417336311656936031122249937969999226781732358023111862644575299135758175008199839236284615249881088960232244362173771618086357015468484058622329792853875623486556440536962622018963571028812361567512543338303270029097668650568557157505516727518899194129711337690149916181315171544007728650573189557450920330185304847113818315407324053319038462084036421763703911550639789000742853672196280903477974533320468368795868580237952218629120080742819551317948157624448298518461509704888027274721574688131594750409732115080498190455803416826949787141316063210686391511681774304792596709376

[Yadryara]

venco, ну а что насчёт 6-ти бросков скажете? Ваш треугольник только до 5 доходит.

-- 18.09.2021, 20:48 --

Dmitriy40

Если вот так подправить код, то почему-то выдаёт $247$. А разве должна не $236$?

nn=9; kk=6;
T=matrix(nn, kk); T[1,1]=1;
{rT(n,k)=
   if(k<0 || k>n, return(0));
   if(k==0 || k==n || n==0, return(1));
  2*rT(n-1,k)+rT(n-1,k-1)-2*rT(n-2,k-1)+rT(n-k-1,k-1)-rT(n-k-2,k);}
for(n=2,kk+2, for(k=1,min(n,kk), T[n,k]=rT(n,k)););
for(n=kk+3,nn, T[n,1]=2*T[n-1,1]+1-2*1+1-T[n-1-2,1];
for(k=2,kk, T[n,k]=2*T[n-1,k]+T[n-1,k-1]-2*T[n-2,k-1]+T[n-k-1,k-1]-T[n-k-2,k]););
print(vecsum(T[nn-1,1..5]));

[venco]

Yadryara в сообщении #1532017 писал(а):

venco, ну а что насчёт 6-ти бросков скажете? Ваш треугольник только до 5 доходит.

Да нет, всё сошлось.
Для произвольных повторов количество вариантов длины $n$ с повтором длины $k$ очевидно равно удвоенному количеству разбиений числа $n$ на слагаемые с максимальным слагаемым $k$.
Для повторов единицы - допишем в конце $0$ и поделим последовательность после каждого нуля. Получится разбиение $n+1$ на слагаемые с максимальным $k+1$.

[Yadryara]

venco, хорошо. А я тем временем, видимо, ошибку нашёл у Dmitriy40. Суммирование надо начинать с первого числителя, а программа начинает со второго. При $n=6$ полное совпадение, а затем, начиная с $n=7$ погрешность начинает расти и к $n=600$ становится космической. При $n=9$ она, как я уже отметил, равна $11$.

То есть суммируются не $1 + 54 + 94 + 59 + 28$, а $54 + 94 + 59 + 28 + 12$

[Dmitriy40]

Yadryara
Да, в том коде значения оказались с нулевого смещения, правильный код вот:

nn=600;kk=6;
T=matrix(nn,kk);
{rT(n,k)=
   if(k<0 || k>n, return(0));
   if(k==0 || k==n || n==0, return(1));
    2*rT(n-1,k)+rT(n-1,k-1)-2*rT(n-2,k-1)+rT(n-k-1,k-1)-rT(n-k-2,k);
}
for(n=1,kk+1, T[n,1]=1; for(k=2,min(n,kk), T[n,k]=rT(n-1,k-1)); );
for(n=kk+2,nn, T[n,1]=1; for(k=2,kk, T[n,k]=2*T[n-1,k] + T[n-1,k-1] - 2*T[n-2,k-1] + T[n-k,k-1] - T[n-k-1,k]); );
print(vecsum(2.0*T[nn,1..5])/2^nn);

Теперь выдаёт и всю матрицу правильно, и вероятность стала не 0.7%, а 36ppm, как и у venco и в прогонах у provincialka. Так что да, считал неправильно (точнее для $m=7$ вместо $m=6$ и не учитывал первую $2$).

[Yadryara]

Ну вот, чего ж бежать впереди паровоза. Говорил же надо сначала с маленькими значениями разобраться. Перепроверил последнюю версию программы и настроил её для проверки стат. результатов Уважаемой provincialka. Прекрасно получилось.

provincialka в сообщении #1532000 писал(а):

$$\begin{matrix} 5& 6 & 7 & 8 & 9 & 10 & 11 &12 &13&14 & \\ 22& 7585 & 83872 & 216251 & 250036 & 189880 & 117287& 65298 &34544 &17466 & \end{matrix}$$

Мат. ожидания:

$$\begin{matrix} 5& 6 & 7 & 8 & 9 & 10 & 11 &12 &13&14 & \\ 36& 7389 & 84113 & 216422 & 249970 & 190294 & 117278 & 65021 & 34196 & 17519 & \end{matrix}$$

А вот и код. За основу по-прежнему берётся A048004.

nn=600;kk=14;
T=matrix(nn,kk);
{rT(n,k)=
   if(k<0 || k>n, return(0));
   if(k==0 || k==n || n==0, return(1));
   2*rT(n-1,k)+rT(n-1,k-1)-2*rT(n-2,k-1)+rT(n-k-1,k-1)-rT(n-k-2,k);}
for(n=1,kk+1, T[n,1]=1; for(k=2,min(n,kk), T[n,k]=rT(n-1,k-1)); );
for(n=kk+2,nn, T[n,1]=1;for(k=2,kk,T[n,k]=2*T[n-1,k]+T[n-1,k-1]-2*T[n-2,k-1]+T[n-k,k-1]-T[n-k-1,k]););
print();print("   ",2.*T[nn,5..14]/2^nn*10^6);print();

[Yadryara]

venco в сообщении #1532011 писал(а):

Для $n=600$ вероятности получить максимальный повтор $1..6$ равны:
$4.8198\cdot 10^{-181}, 8.6123\cdot 10^{-56}, 1.83646\cdot 10^{-22}, 2.76136\cdot 10^{-10}, 3.60578\cdot 10^{-05}, 0.00738934$

Да, и с этими значениями полное совпадение. Добавил по 4-5 значащих цифр справа, чтобы было понятно, что именно это тоже посчитано:

$1. \qquad 4.819839730\cdot 10^{-181}$,

$2. \qquad 8.612304675\cdot 10^{-56}$,

$3. \qquad 1.836462902\cdot 10^{-22}$,

$4. \qquad 2.761355662\cdot 10^{-10}$,

$5. \qquad 3.605779071\cdot 10^{-05}$,

$6. \qquad 7.389340284\cdot 10^{-03}$

nn=600;kk=14;
T=matrix(nn,kk);
{rT(n,k)=
   if(k<0 || k>n, return(0));
   if(k==0 || k==n || n==0, return(1));
   2*rT(n-1,k)+rT(n-1,k-1)-2*rT(n-2,k-1)+rT(n-k-1,k-1)-rT(n-k-2,k);}
for(n=1,kk+1, T[n,1]=1; for(k=2,min(n,kk), T[n,k]=rT(n-1,k-1)); );
for(n=kk+2,nn, T[n,1]=1;for(k=2,kk,T[n,k]=2*T[n-1,k]+T[n-1,k-1]-2*T[n-2,k-1]+T[n-k,k-1]-T[n-k-1,k]););
print();print("   ",2.*T[nn,1..6]/2^nn);print();

mihaild в сообщении #1531978 писал(а):

Вероятность того, что из $600$ бросков максимальная серия из орлов будет иметь длину ровно $n$ - на картинке.

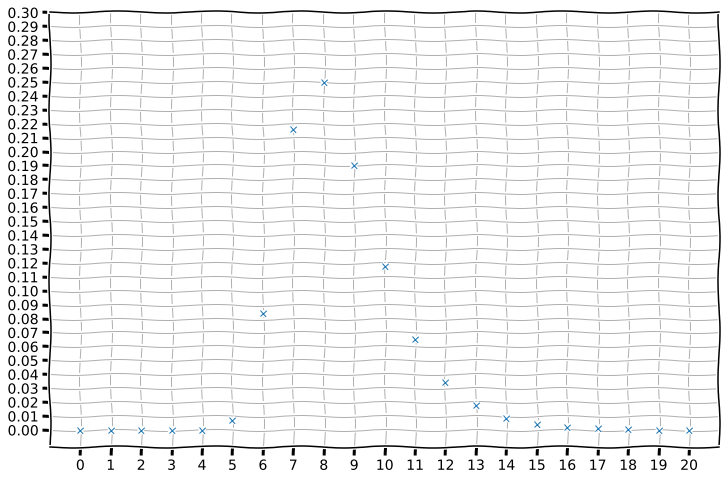
Если, не трогая рисунок, сдвинуть нижнюю шкалу на $1$ влево, получим те самые вероятности, что участвуют и в предыдущем посте и в нынешнем. Потому что программа на PARI не считает именно орлы.

venco в сообщении #1532014 писал(а):

Я оценил ассимптотику и получил, что уже для 10000 бросков вероятность получить максимум 6 повторов $1.66722\cdot10^{-36}$

У меня очень близкий результат прямым подсчётом:

$6. \qquad 1.667199293\cdot 10^{-36}$

nn=10000;kk=14;
T=matrix(nn,kk);
{rT(n,k)=
   if(k<0 || k>n, return(0));
   if(k==0 || k==n || n==0, return(1));
   2*rT(n-1,k)+rT(n-1,k-1)-2*rT(n-2,k-1)+rT(n-k-1,k-1)-rT(n-k-2,k);}
for(n=1,kk+1, T[n,1]=1; for(k=2,min(n,kk), T[n,k]=rT(n-1,k-1)); );
for(n=kk+2,nn, T[n,1]=1;for(k=2,kk,T[n,k]=2*T[n-1,k]+T[n-1,k-1]-2*T[n-2,k-1]+T[n-k,k-1]-T[n-k-1,k]););
print();print("   ",2.*T[nn,6]/2^nn);print();

[Dmitriy40]

Yadryara в сообщении #1532068 писал(а):

У меня очень близкий результат прямым подсчётом:

Хочу обратить Ваше внимание что Вы иногда указываете не совсем ту вероятность, о которой утверждаете: в матрице $T[n,k]$ сидят частоты выпадения длин не максимум $k$, а ровно $k$, потому если хотите частоту длин максимум $k$, надо сложить её со всеми меньшими $k$ (как у меня в коде и было vecsum). Поправка для больших $n$ исчезающе мала (десяток и более порядков), однако для малых $n$ будет заметна.

Например $P(600,6)=0.007389340284124275425954794433$, но $\sum_{k=0}^6 P(600,k) = 0.007425398350972517534375923643$, разница составляет $0.00003605806684824210842112921$ или почти $0.5\%$ погрешности, почти точно (4 одинаковых знака) значение $P(600,5)=0.00003605779071267586675086922$. Т.е. для погрешности менее 1% $n=600$ уже следует считать малым.

(Улучшение программы)

Если попытаться считать очень большие $n$, типа миллионов или миллиардов, то не хватит памяти под матрицу $T[]$. Тогда можно заметить что для расчёта $T[n,\ldots]$ требуются элементы не менее чем $T[n-k-1,\ldots]$, что позволяет хранить лишь их, в количестве $k+2$ строк. Модификация кода не слишком сложна, но или замедлит расчёты (если делать сдвигом матрицы) или потребует аккуратности (если реализовать кольцевую структуру) или нужно найти в PARI готовую удобную структуру (типа хэш дерева).

При расчёте больших $k$ первый цикл быстро становится непрактичным из-за глубокой рекурсии в $rT()$, часто не нужной. Например $k=15$ считается пару секунд, а $k=20$ требует уже 3 минуты. Тогда можно подправить код $rT()$ чтобы она не вызывалась рекурсивно если индексы гарантированно не уходят меньше единицы, например вот так:

{rT(n,k)=
   if(k<0 || k>n || n<0, return(0));
   if(k==0 || k==n || n==0, return(1));
    2*T[n,k+1] + T[n,k] - 2*T[n-1,k] + if(n>k, T[n-k,k], rT(n-k-1,k-1)) - if(n-1>k, T[n-k-1,k+1], rT(n-k-2,k));
}
for(n=1,nn, for(k=1,min(n,kk), T[n,k]=rT(n-1,k-1); ); );

Тут добавлены проверки, заменяющие длинные рекурсии на обращение к матрице. В результате время вычисления $k=20$ уменьшилось с трёх минут до 0.15 секунды и даже для $k=10000$ составляет чуть более секунды.
И это же позволило вообще отказаться от деления на два цикла и всё заполнение матрицы делать простым первым, разница в вызове функции и четвёрке условных операторов несущественна (вычисления $n=600,k=100$ занимают в любом случае менее секунды, $n=10000,k=100$ занимают 5.2 секунды против 4.3 с двумя циклами).

[Yadryara]

Dmitriy40 в сообщении #1532098 писал(а):

Хочу обратить Ваше внимание что Вы иногда указываете не совсем ту вероятность, о которой утверждаете:

А можно хоть один пример?

Dmitriy40 в сообщении #1532098 писал(а):

в матрице $T[n,k]$ сидят частоты выпадения длин не максимум $k$, а ровно $k$, потому если хотите частоту длин максимум $k$, надо сложить её со всеми меньшими $k$ (как у меня в коде и было vecsum).

Я в курсе. Я поэтому довольно часто и убирал vecsum. Потому что мне часто нужны были именно эти числа, а не их сумма. Я за этим внимательно следил.

[Dmitriy40]

Yadryara в сообщении #1532104 писал(а):

А можно хоть один пример?

Например вот здесь:

Yadryara в сообщении #1532068 писал(а):

venco в сообщении #1532011 писал(а):

Для $n=600$ вероятности получить максимальный повтор $1..6$ равны:
$4.8198\cdot 10^{-181}, 8.6123\cdot 10^{-56}, 1.83646\cdot 10^{-22}, 2.76136\cdot 10^{-10}, 3.60578\cdot 10^{-05}, 0.00738934$

Да, и с этими значениями полное совпадение. Добавил по 4-5 значащих цифр справа, чтобы было понятно, что именно это тоже посчитано:
$1. \qquad 4.819839730\cdot 10^{-181}$,
$2. \qquad 8.612304675\cdot 10^{-56}$,
$3. \qquad 1.836462902\cdot 10^{-22}$,
$4. \qquad 2.761355662\cdot 10^{-10}$,
$5. \qquad 3.605779071\cdot 10^{-05}$,
$6. \qquad 7.389340284\cdot 10^{-03}$

Вы оба указали не сумму всех меньших вероятностей, а сами вероятности, (да, и venco тоже, хотя прямо сказал про максимальный повтор), сравните числа для $k>4$ со своими выше:

P(600,1)=4.819839730205768 e-181 vs Sum(P(600,1...1))=4.819839730205768 e-181
P(600,2)=8.612304675229292 e-56 vs Sum(P(600,1...2))=8.612304675229292 e-56
P(600,3)=1.836462902103414 e-22 vs Sum(P(600,1...3))=1.836462902103414 e-22
P(600,4)=2.761355662414866 e-10 vs Sum(P(600,1...4))=2.761355662416703 e-10
P(600,5)=3.605779071267587 e-5 vs Sum(P(600,1...5))=3.605806684824211 e-5
P(600,6)=7.389340284124275 e-3 vs Sum(P(600,1...6))=7.425398350972518 e-3

[Yadryara]

Dmitriy40 в сообщении #1532107 писал(а):

Вы оба указали не сумму всех меньших вероятностей, а сами вероятности,

Совершенно верно, мы сравнивали одно и то же. Не сумму. Где же пример?

[Dmitriy40]

Yadryara
Вы сравнили друг с другом, всё сошлось, но назвали величины неправильно, это не максимум $k$, а ровно $k$. Ошибся venco, Вы с ним согласились, не поправили.
Ладно, раз понимаете, то считайте моё напоминание неактуальным или придиркой.

[mihaild]

Dmitriy40 в сообщении #1532098 писал(а):

Если попытаться считать очень большие $n$, типа миллионов или миллиардов, то не хватит памяти под матрицу $T[]$

Да и считать её целиком не нужно. Следующая строка получается из предыдущих линейно, поэтому задача сводится к вычислению $n$-й степени матрицы $k \times k$.

Вообще я перестал понимать, что в точности обсуждается?

[Dmitriy40]

Да уже ничего, все разногласия в цифрах устранены, что задача не для решения "на бумажке" давно стало понятно.