Поэтому модель, где какие-то заряды равномерно заполняют окружность на границе диска, а какие-то заряды противоположного знака равномерно размазаны по диску, здесь уместна.
Как оказалось, что это не так. На диске сила отталкивания зарядов от центра пропорциональна квадрату расстояния от центра. Поэтому логично предположить, что отрицательно заряженные заряды будут распределены на диске с плотностью, которая будет пропорционально квадрату расстояния от центра.
Другое дело, как найти заряд на окружности диска?
Простые рассуждения, связанные с балансом сил, показывают, что этот заряд равен заряду, вычисленному несколько постов назад. С учётом того, что отрицательный заряд размазан по диску квадратично, предыдущую оценку числового коэффициента в формуле удалось понизить в три раза с
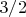
до

. Это в СГСЭ. А в СИ этот коэффициент надо разделить на

.
profilescit. А где по вашей ссылке можно найти официальный ответ к задаче? Нашёл только кучу официальных подсказок и три труднопонимаемых решения участников.