Составить кратный интеграл

[TemplateRLC]

Здравствуйте
Есть закон Джоуля-Ленца: $Q=I^2 \cdot R \cdot t$
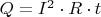
Если меняется время только время, то Q найти легко:

$$Q=\int\limits_{t_1}^{t_2}I^2\cdot R \cdot t dt$$

А если меняется величина тока, сопротивление от температуры и время, то я могу перейти к кратному интегралу в следующем виде:

$$Q=\int\limits_{I_1}^{I_2} \int\limits_{R_1}^{R_2} \int\limits_{t_1}^{t_2} I^2\cdot R \cdot t dI dR dt$$

Или нет?
Просто во всех теориях про кратные интегралы там сначала у внутреннего интеграла в нижнем и верхнем пределе переменные, а потом уже значения. А мне надо значения у всех переменных
(пример как в учебниках подаются кратные интегралы):
$\int\limits_{-2}^{0}dx \int\limits_{x+2}^{\sqrt{4-x^2}}f(x,y)dy$
То есть присутствует ограничения одной переменной через другую у функции( не знаю как правильно сказать) а у меня тут функция Q трех переменных, которые друг друга никак не ограничивают: ток растет от ЭДС катушки, сопротивление меняется от температуры, время задается по часам.
Буду рад помощи, спасибо.

UPD: о каких разных размерностях идет речь?

[Pphantom]

TemplateRLC в сообщении #1510114 писал(а):

Есть закон Джоуля-Ленца: $Q=I^2 \cdot R \cdot t$
Если меняется время только время, то $Q$ найти легко:

$$Q=\int\limits_{t_1}^{t_2}I^2\cdot R \cdot t dt$$

Что легко - это хорошо, но вас не смущает то, что $Q$ в первом равенстве и $Q$ во втором равенстве имеют как минимум разные размерности?

Дальше та же проблема становится еще более яркой. Попробуйте изложить физический смысл того, что вы делаете, когда пишете интегралы.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- cм. выше;
- ну и заодно надо правильно набрать формулы/обозначения, учебник не обязательно "цитировать" в виде картинки (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.