Тогда
![$[a, b] = \prod\limits_{p | ab} p^\max\left(f(p, a), f(p, b)\right)$ $[a, b] = \prod\limits_{p | ab} p^\max\left(f(p, a), f(p, b)\right)$](https://dxdy-01.korotkov.co.uk/f/8/5/1/8514be6a6eca5f900a384b3dc81d8fdc82.png)
.
Пусть мы находимся в

и ищем
![$[3 , 4]$ $[3 , 4]$](https://dxdy-04.korotkov.co.uk/f/3/1/7/3179fd1cce87a7a1f5f791526a48aafb82.png)
. Выписываем все простые, которые делят

:

Далее

,

. Запишем произведение


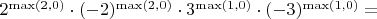

, а надо 12. Тут я думаю нужно условие на ассоциированные: их не надо считать несколько раз.
Обозначить

и доказать, что любое общее кратное

элементов

и

будет делиться на

.
У меня так получилось. Возьмем произвольные

.

.

,

Положим

. Легко показать, что

является общим кратным

и

. Докажем, что

делит любое общее кратное

элементов

и

.
1)

.
2)

чтд.
-- 06.03.2021, 21:15 --Это неважно, при поиске НОК ассоциированные элементы можно не различать.
Т.е. это и есть то ограничение на ассоциированные, о котором я выше написал? Если так, то тогда все понятно.