Среднее гармоническое (планиметрия) -- https://dxdy.ru/topic8541

[ircicq]

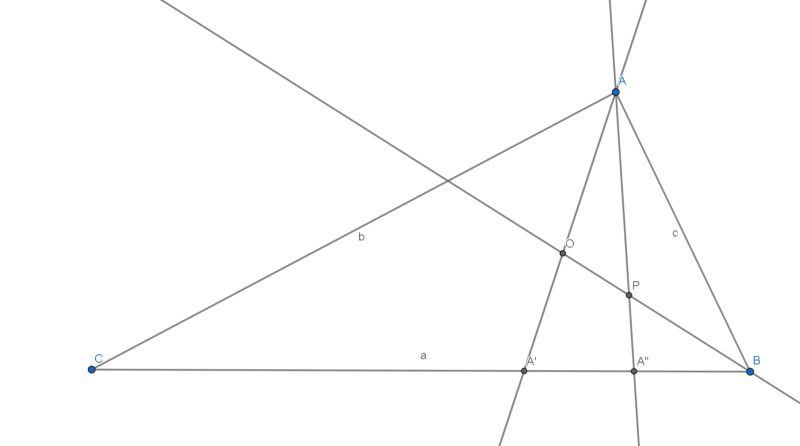
△ABC ~ △A'AC => AA' = $\frac{bc}{a}$
△ABA' - равнобедренный => BA' = AA' = $\frac{bc}{a}$
В равнобедренном △ABA' биссектрисы равных углов равны:
AA'' = BO
△A''PB = △OPA и они подобны ABC => $\frac{PB}{OP}$ = $\frac{PB}{PA''}$ = $\frac{a}{c}$ (1)

т.к. P - точка пересечения биссектрис △ABA', то
$\frac{PB}{OP}$ = $\frac{c + A'B}{AA'}$ = (c + bc/a) / (bc/a) = $\frac{a}{b}$ + 1

приравнивая с (1):

$\frac{a}{c}$ = $\frac{a}{b}$ + 1

c = 1/(1/a + 1 /b) (половина среднего гармонического, ЧТД)

[Lia]

ircicq
Ну если уж Вы решили разместить решение в архивной теме через шесть лет после последнего сообщения там, то приведите его в порядок, пожалуйста. Наберите формулы.

Сообщение перемещено в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.