Связь между прямой и двойственной задач ЛП

innokentijglum · 03.12.2020, 21:39

Доброго времени суток!

Столкнулся со следующей проблемой: всегда ли можно по вектору решения двойственной задачи линейного программирования найти вектор решения прямой задачи линейного программирования?

Дана прямая задача:

$\omega(x)=3x_1+5x_2+4x_2 \rightarrow \min$

$x_1+2x_2+3x_3 \ge 1$
$2x_1+3x_2+x_3 \ge 1$
$3x_1+x_2+2x_3 \ge 1$
$6x_1+6x_2+6x_3 \ge 1$
$2x_1+4x_3 \ge 1$
$x_1, x_2, x_3 \in \mathbb{R}$

Строим для нее двойственную:

$z(y)=y_1+y_2+y_3+y_4+y_5 \rightarrow \max$

$$y_1+2y_2+3y_3+6y_4+2y_5 = 3$$

$y_1, y_2, y_3, y_4, y_5 \ge 0$

Решение двойственной задачи:
$z^{\star}=2$ , $y^{\star}=(1, 1, 0, 0, 0)$ .

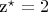
И тут я не понимаю, как применять двойственность, понятно, что $\omega^{\star}=z^{\star}=2$ (по первой теореме двойственности), но как по вектору $y^{\star}=(1, 1, 0, 0, 0)$ найти вектор $x^{\star}$ ? Меня смущает, что в прямой задаче все переменные из $\mathbb{R}$ , и в двойственной все ограничения - равенства. (Непонятно, как применять вторую теорему двойственности).

То есть, если в прямой все переменные ограничены по знаку (больше, либо равны нулю) и ограничения-неравенства, то в двойственной задаче также все переменные больше, либо равны нулю, и все ограничения-неравенства, то понятно как рассуждать.

Например,

опять же прямая задача:

$\omega(x)=8x_1+6x_2-3x_3 \rightarrow \max$

$3x_1+x_2-x_3 \le 1$
$x_1+2x_2+x_3 \le 1$
$x_1, x_2, x_3 \ge 0$

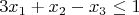
Двойственная задача:

$z(y)=y_1+y_2 \rightarrow \min$

$3y_1+y_2 \ge 8$
$y_1+2y_2 \ge 6$
$-y_1+y_2 \ge -3$
$y_1, y_2 \ge 0$

Решение двойственной:
$z^{\star}=4$ , $y^{\star}=(2, 2)$ .

Согласно первой теореме двойственности, оптимальное значение целевой функции прямой задачи равно
$\omega^{\star}=z^{\star}=4$ .

Применим вторую теорему двойственности. Подставим оптимальные значения переменных $y^{\star}=(2, 2)$ в систему ограничений прямой задачи.
$3y_1+y_2=3 \cdot 2+2=8;$
$y_1+2y_2=2+2 \cdot 2=6;$
$$-y_1+y_2=-2+2=0 > -3.$$

Поскольку третья строка является строгим неравенством (не являются равенством), то $x_3=0$ .

Поскольку $y_1 \ne 0$ и $y_2 \ne 0$ , то 1-я и 2-я строки двойственной задачи являются равенствами:
$\begin{cases} 3x_1+x_2-x_3=1\\ x_1+2x_2+x_3=1 \end{cases}$

Подставим найденное значение $x_3=0$ .

Решаем систему уравнений.
$x_1=1-2x_2$ ;
$3(1-2x_2)+x_2=1$ ;
$3-6x_2+x_2=1$ ;
$5x_2=2; x_2=\frac{2}{5}$ ;
$x_1=1-2x_2=1-\frac{4}{5}=\frac{1}{5}$ .

Итого, $x^{\star}=(\frac{1}{5}, \frac{2}{5})$ .

Чтобы получить векторы решений для первой пары задач я пробовал таким образом рассуждать:
так как в оптимальном решении $y^{\star}=(1, 1, 0, 0, 0)$ $y_1 \ne 0$ и $y_2 \ne 0$ , то первые 2 ограничения обратятся в равенства по второй теореме двойственности, т.е.

$$ x_1+2x_2+3x_3=1$$

.

Откуда

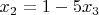
Если же, что напрашивается, подставить эти соотношения в целевую функцию $\omega(x)$ , зная что $\omega^{\star}=2$ , то получим:

$$3x_1+5x_2+4x_3=2$$

... и оптимального значения для $x_3$ мы не получаем...

В общем, я не понимаю, как для первой пары задач по вектору решения двойственной задачи найти вектор решения прямой. И, вообще, можно ли это каким-либо образом сделать? Помогите, пожалуйста!

Pphantom · 04.12.2020, 11:05

i

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы) - все внутристрочные формулы надо окружить долларами (один спереди, один сзади).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

Научный форум dxdy

Связь между прямой и двойственной задач ЛП